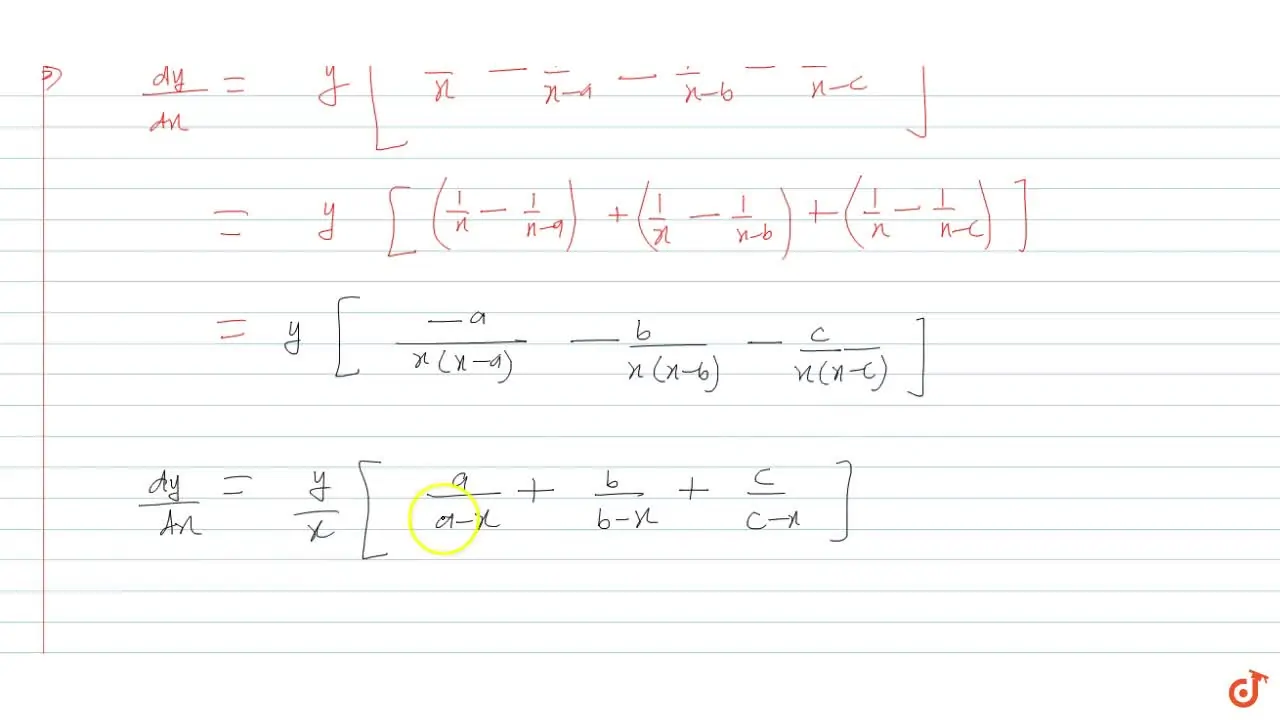If y=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1 find dydx
y=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+c+x−cx−c
=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+xx−c
ax2(x−a)(x−b)(x−c)+bx+x(x−b)(x−b)(x−c)
=ax2+x2(x−1)(x−a)(x−b)(x−c)
y=a3(x−a)(x−b)(x−c)
logy=logx3−{log(x−a)+log(x−b)+log(x−c)}
logy=3logx−log(x−a)−log(x−b)−log(x−c)
1y⋅dydx=3x−1x−a−1x−b−1x−c
dydx=y[3x−1x−a−1x−b−1x−c]
=y[(1x−1x−a)+(1x−1x−b)+(1x−1x−c)]
=y[−ax(x−a)−bx(x−b)−cx(x−c)]
=yx[aa−x+bb−x+cc−x]
Answer
Related Playlists
- BOOK - RD SHARMACHAPTER - DIFFERENTIALS, ERRORS AND APPROXIMATIONSEXERCISE - Solved Examples And Exercises102videos
DIFFERENTIALS, ERRORS AND APPROXIMATIONS
- BOOK - RD SHARMACHAPTER - DIRECTION COSINES AND DIRECTION RATIOSEXERCISE - Solved Examples And Exercises67videos
DIRECTION COSINES AND DIRECTION RATIOS
Similar Questions
If y=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1 find dydx
View SolutionIf y=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1 then y'y=
View SolutionIf y=ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1, then prove that y'y=1x[aa−x+bb−x+cc−x]
View SolutionProve that
ax2(x−a)(x−b)(x−c)+bx(x−b)(x−c)+cx−c+1
=x3(x−a)(x−b)(x−c).View Solutionx3(x−a)(x−b)(x−c)=1+Ax−a+Bx−b+Cx−c then A=
View SolutionLet y=2x2(x−2)(x−3)(x−4)+3x(x−3)(x−4)+xx−4 .If xydydx=a2−x+b3−x+c4−x then a+b+c is
View Solutiona2x−a+b2x−b+c2x−c+a+b+cax−a+bx−b+cx−c
View SolutionIf y=(x+a)(x+b)(x+c)(x+d) / (x-a)(x-b)(x-c)(x-d) then the value of dy/dx:
View SolutionDifferentiate (xaxb)a+b⋅(xbxc)b+c⋅(xcxa)c+a with respect to x.
View SolutionLet P(x)=(x−a)(x−b)(c−a)(c−b)c2+(x−b)(x−c)(a−b)(a−c)a2+(x−c)(x−a)(b−c)(b−a)b2
Prove that P(x) has the property that P(y)=y2 for all y∈R.View Solution