If z a complex number satisfying ∣∣z3+z−3∣∣≤2, then the maximum possible value of ∣∣z+z−1∣∣ is -
A
2
B
3√2
C
2√2
D
1
Video Solution
Text Solution
The correct Answer is:A
∣∣z3+z−3∣∣≤2
∣∣∣z3+1z3∣∣∣≤2
∣∣∣(z+1z)(z2+1z2)∣∣∣≤2
∣∣
∣∣(z+1z)((z+1z)2−3)∣∣
∣∣≤2
∣∣∣z+1z∣∣∣∣∣∣(z+1z)2−3∣∣∣≤2
∣∣∣z+1z∣∣∣{∣∣∣z+1z∣∣∣2−3∣}≤2 {∵∣∣z1−z2∣∣≤∣∣|z1|−z2∣∣∣}
t∣∣t2−3∣∣≤2 (t≤0)where t=∣∣∣z+1z∣∣∣
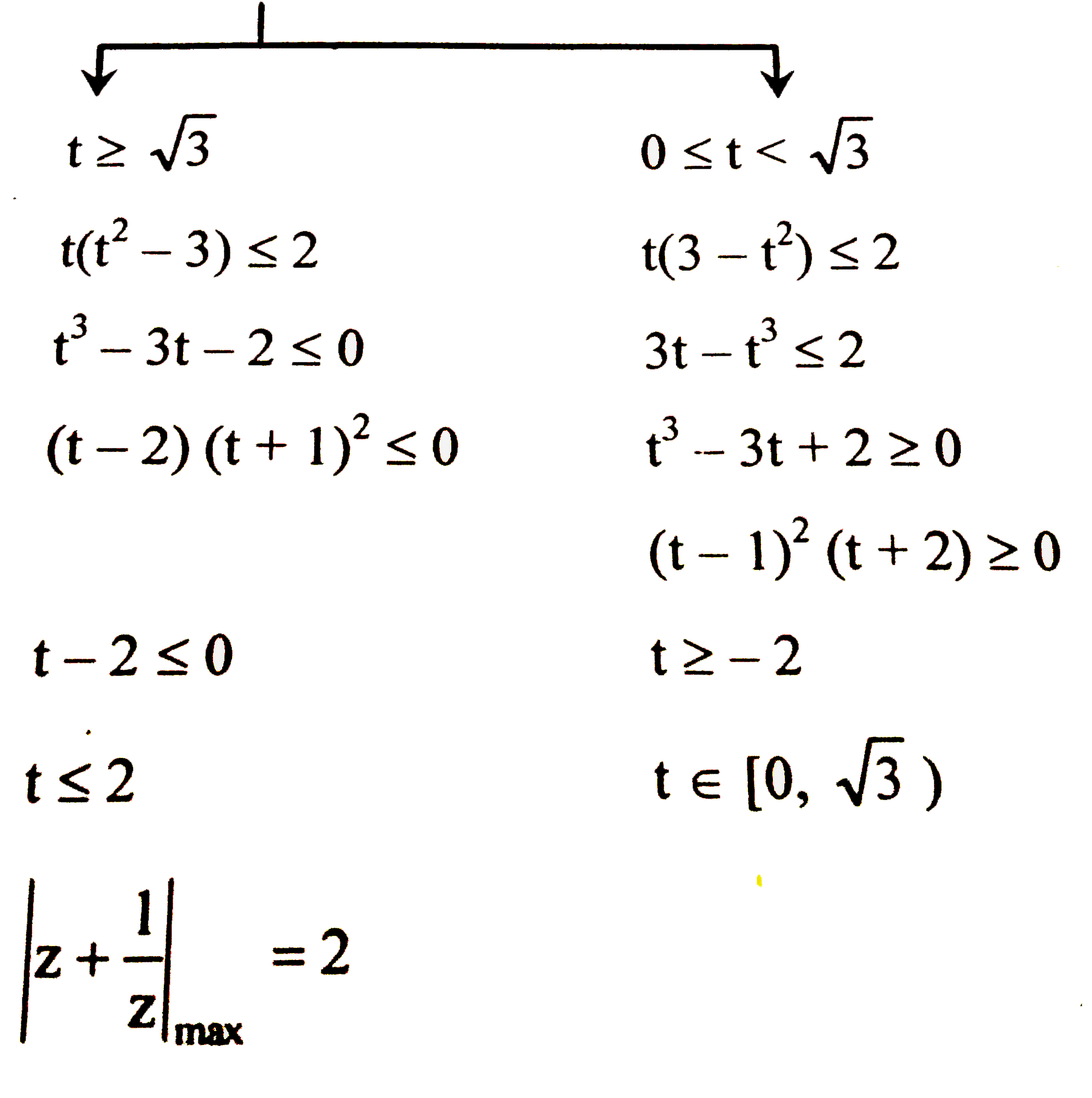
|
Similar Questions
Knowledge Check
If z is a complex number satisfying ∣∣z2+1∣∣=4|z|, then the minimum value of |z| is
A2√5+4B2√5−4C√5−2Dnone of theseIf z is any complex number satisfying |z−3−2i|≤1 then the minimum value of |2z−6+5i| is
A5B6C7D0Let z be a complex number such that |z| = 2, then maximum possible value of ∣∣∣z+2z∣∣∣ is
A1B2C3D4
If z is any complex number satisfying |z−3−2i|≤2 then the maximum value of |2z−6+5i| is
View SolutionLet a=3+4i,z1andz2 be two complex numbers such that |z1|=3and|z2−a|=2, then maximum possible value of |z1−z2| is ___________.
View SolutionNumber of complex numbers z satisfying z3=¯z is
View SolutionIf z is a complex number satisfying the equaiton z6−6z3+25=0, then the value of |z| is
View SolutionFor the complex number z satisfying the condition ∣∣∣z+2z∣∣∣=2, the maximum value of |z| is
View Solution
