If z1,z2 are two complex numbers representing two consecutive vertices of a square then what is the complex number represented by the centre of the square ?
To find the complex number that represents the center of a square formed by two consecutive vertices represented by complex numbers z1 and z2, we can follow these steps:
1. Understanding the Geometry:
- Let z1 and z2 be two consecutive vertices of the square. The center of the square is the midpoint of the line segment connecting the two diagonally opposite vertices.
2. Finding the Midpoint:
- The center of the square can be found by taking the average of the coordinates of the two vertices. The formula for the midpoint z of two points z1 and z2 in the complex plane is given by:
z=z1+z22
3. Understanding the Rotation:
- Since z1 and z2 are consecutive vertices, the center of the square can also be derived using the concept of rotation. To find the center, we can rotate the vector from z1 to z2 by 90 degrees around the center.
4. Using Complex Numbers for Rotation:
- The rotation of a complex number z by 90 degrees counterclockwise can be achieved by multiplying it by i (where i is the imaginary unit). Thus, the vector from z1 to z2 can be expressed as z2−z1.
5. Setting Up the Equation:
- To find the center z, we can express it as:
z−z1=i(z2−z1)
- Rearranging gives:
z=z1+i(z2−z1)
6. Simplifying the Expression:
- This can be simplified to:
z=z1+iz2−iz1=(1−i)z1+iz2
7. Final Result:
- After rationalizing and simplifying, we find that the center of the square can also be expressed as:
z=z1+z22+iz1−z22
Conclusion:
The complex number representing the center of the square formed by the vertices z1 and z2 is:
z=z1+z22+iz1−z22
- Let z1 and z2 be two consecutive vertices of the square. The center of the square is the midpoint of the line segment connecting the two diagonally opposite vertices.
- The center of the square can be found by taking the average of the coordinates of the two vertices. The formula for the midpoint z of two points z1 and z2 in the complex plane is given by:
z=z1+z22
- Since z1 and z2 are consecutive vertices, the center of the square can also be derived using the concept of rotation. To find the center, we can rotate the vector from z1 to z2 by 90 degrees around the center.
- The rotation of a complex number z by 90 degrees counterclockwise can be achieved by multiplying it by i (where i is the imaginary unit). Thus, the vector from z1 to z2 can be expressed as z2−z1.
- To find the center z, we can express it as:
z−z1=i(z2−z1)
- Rearranging gives:
z=z1+i(z2−z1)
- This can be simplified to:
z=z1+iz2−iz1=(1−i)z1+iz2
- After rationalizing and simplifying, we find that the center of the square can also be expressed as:
z=z1+z22+iz1−z22
The complex number representing the center of the square formed by the vertices z1 and z2 is:
z=z1+z22+iz1−z22
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - A DAS GUPTACHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
224 Videos
- Circular Functions, Identities BOOK - A DAS GUPTACHAPTER - Circular Functions, Identities EXERCISE - Exercise
300 Videos
- Continuity, Differentiability and Graph of FunctionBOOK - A DAS GUPTACHAPTER - Continuity, Differentiability and Graph of FunctionEXERCISE - Exercise
38 Videos
Similar Questions
If z1,z2 are two complex numbers representing consecutive vertices of a regular hexagon then the complex number z3 representing the vertex adjacent to z2. is __________________.
View Solutionz1,z2 are represented by two consecutive vertices of a rhombus, the angle at z1 being π4. Find the complex numbers z3,z4 represented by the other vertices, the vertices z1,z2,z3,z4 being in the anticlockwise sense and origin being the center.
View Solution
Knowledge Check
If z1,z2 are ant two complex number, then :
A|z_1+z_2|ge|z-1|+|z_2|B|z_1+z_2|gt|z-1|+|z_2|C|z_1+z_2|le|z-1|+|z_2|D|z_1+z_2|=|z-1|+|z_2|If z1,z2 are ant two complex number, then :
A|z_1+z_2|ge|z-1|+|z_2|B|z_1+z_2|gt|z-1|+|z_2|C|z_1+z_2|le|z-1|+|z_2|D|z_1+z_2|=|z-1|+|z_2|A square planer complex represented as :
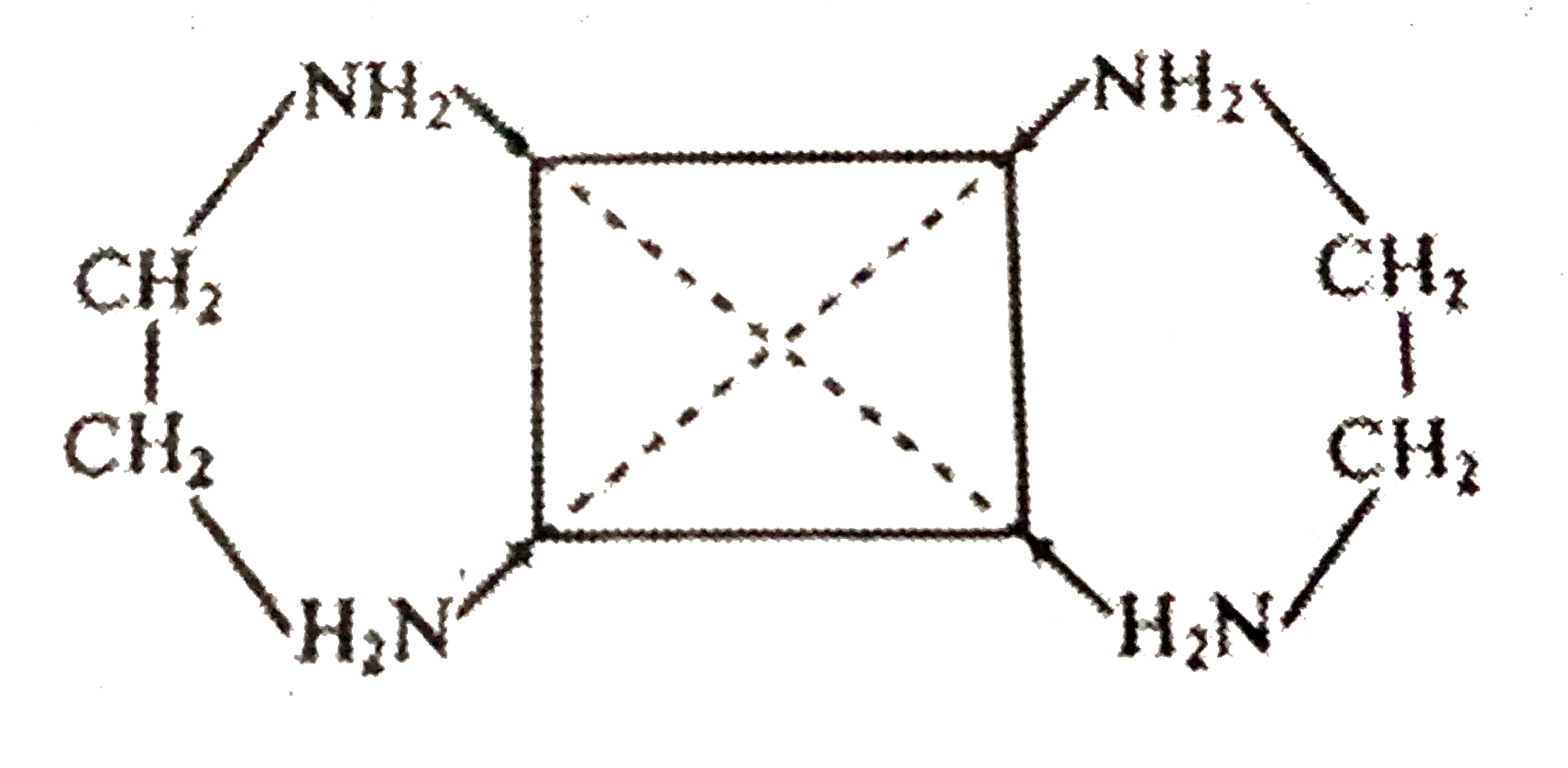 AGeometrical isomerismBOptical isomerismCLinkage isomerismDNone of these
AGeometrical isomerismBOptical isomerismCLinkage isomerismDNone of these
If P(z1),Q(z2),R(z3) and S(z4) are four complex numbers representing the vertices of a rhombus taken in order on the complex plane, which one of the following is held good?
View SolutionIf the complex numbers iz,zandz+izrepresent the three vertices of a triangle, then the area of the triangle is
View SolutionA square planar complex represented as:

View SolutionIf the complex numbers iz, z and z+iz represent the three vertices of a triangle, then the area of the triangle is
View SolutionLet z1,z2 be two complex numbers represented by points on the circle |z1|=1and|z2|=2 respectively then
View Solution
