In ABC, the median AD divides ∠BAC such that ∠BAD:∠CAD=2:1 . Then cos(A3) is equal to sinB2sinC (b) sinC2sinB 2sinBsinC (d) noneoftheseSolution in Tamil
sinB2sinC
sinC2sinB
2sinBsinC
none of these
The correct Answer is:A

Let A3=∠CAD=θ
Now, by m -n theorem,
(1+1)cotα=1cot2θ−1cotθ
or 2cot(B+2θ)=cot2θ−cotθ
or cot(B+2θ)+cotθ=cot2θ−cot(B+2θ)
or sin(B+3θ)sin(B+2θ)sinθ=sinBsin(B+2θ)sin2θ
or sin(B+A)sinθ=sinBsin2θ
⇒sinC=sinB2cosθ
⇒cos.A3=sinB2sinC
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Multiple)
24 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Comprehension)
34 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.11
4 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
15 Videos
Similar Questions
The sides of ABC satisfy the equation 2a2+4b2+c2=4ab+2a⋅ Then the triangle a)isosceles the triangle b)obtuse c)B=cos−1(78) d) A=cos−1(14)
View SolutionGiven that Δ=6,r1=2,r2=3,r3=6
Circumradius R is equal to
View SolutionRegular pentagons are inscribed in two circles of radius 5and 2 units respectively. The ratio of their areas is
View SolutionIt is given that in a group of 4 students, the probability of 2 students not having the same birthday is 0.893. What is the probability that the 2 students have the same birthday?
View SolutionThe area of a right triangle is 6864 sq. units. If the ratio of its legs is 143:24, then the value of r is ______
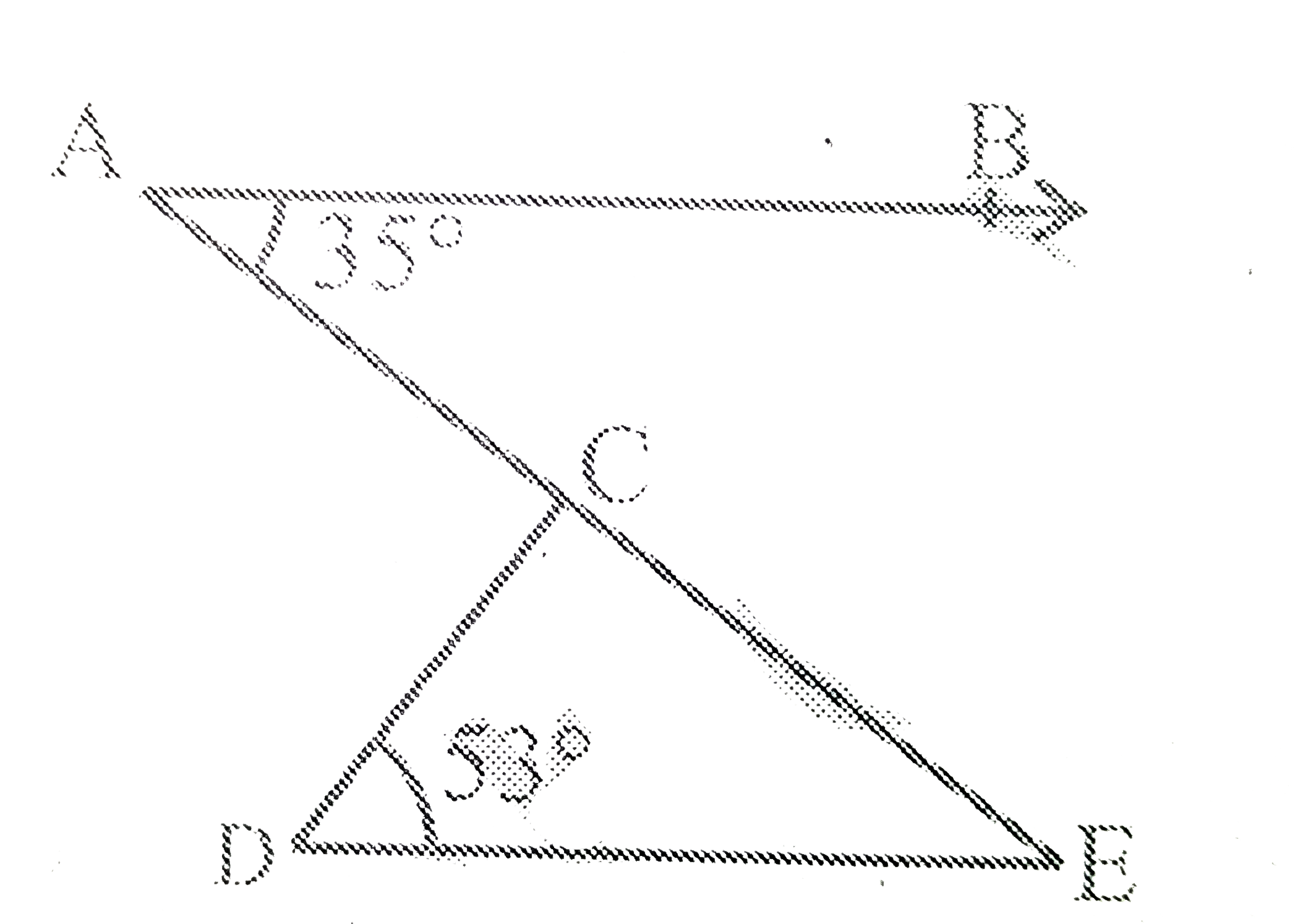
View SolutionIn Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.
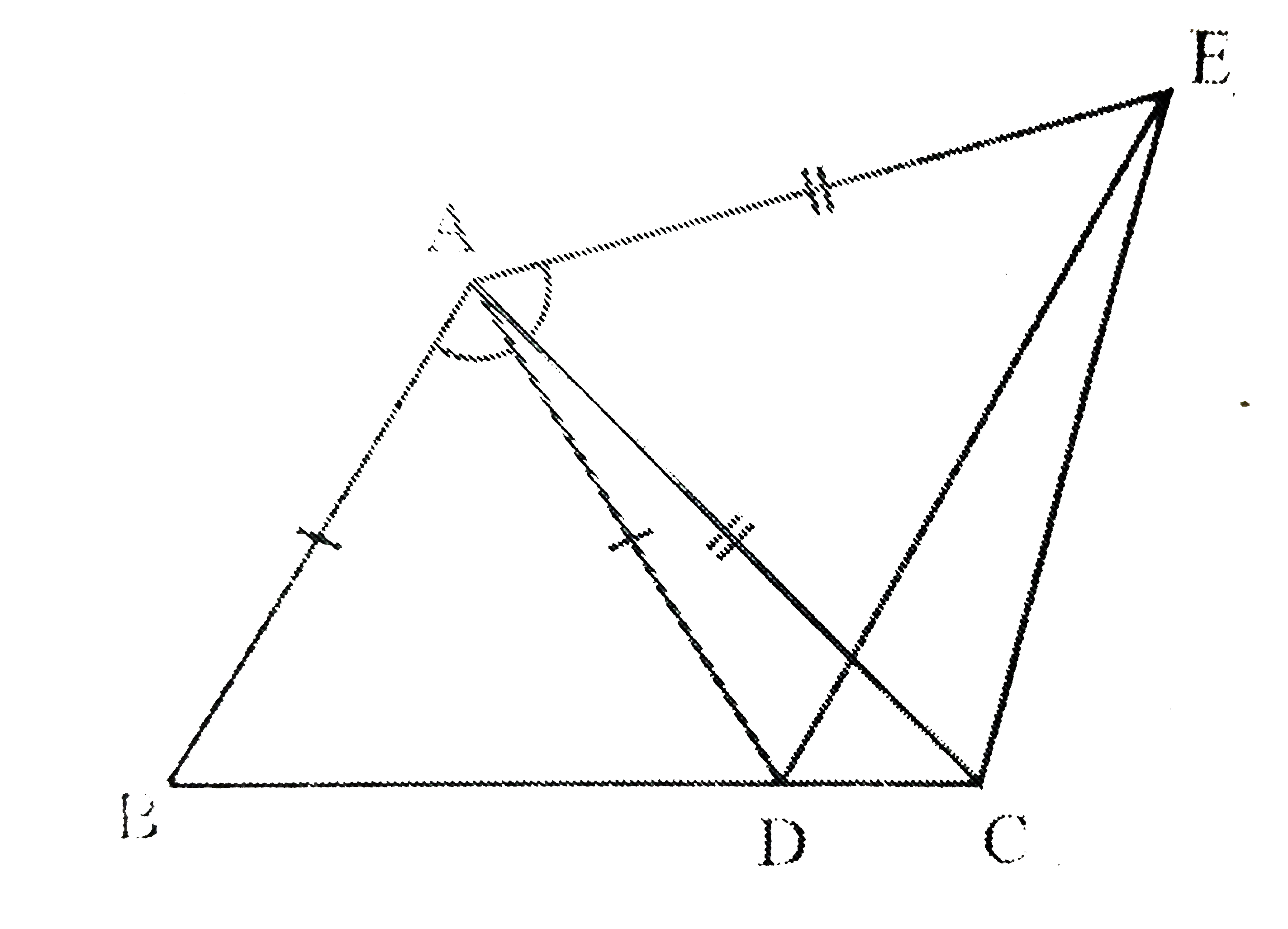
View SolutionIn Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
View SolutionIn Figure, ABC is a triangle in which ∠B=2∠C . D is a point on side BC such that AD bisects ∠BAC and AB=CD.BE is the bisector of ∠B . The measure of ∠BAC is
(a) 720
(b) 730
(c) 740
(d) 960

View SolutionIf A,B,C and D are angles of a quadrilateral and sinA2sinB2sinC2sinD2=14,prove that A=B=C=D=π/2
View SolutionIn Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.

View SolutionIn quadrilateral ABCD, if sin(A+B2)cos(A−B2)+sin(C+D2)cos(C−D2)=2 then find the value of sinA2sinB2sinC2sinD2.
View SolutionIn ABC, the median AD divides ∠BAC such that ∠BAD:∠CAD=2:1 . Then cos(A3) is equal to sinB2sinC (b) sinC2sinB 2sinBsinC (d) noneofthese
View SolutionIn quadrilateral ABCD, if sin(A+B2)cos(A−B2)+sin(C+D2)cos(C−D2)=2 then find the value of sinA2sinB2sinC2sinD2.
View SolutionIn a ABC,D and E are points on sides ABandAC respectively such that BD=CE. If ∠B=∠C, show that DE∣∣BC.
View SolutionThe sides BC, CA and AB of a triangle ABC, are produced in order, forming exterior angles ∠ACD, ∠BAE and ∠CBF. Show that ∠ACD+ ∠BAE+ ∠CBF=3600
View SolutionIn Figure, AE bisects ∠CAD and ∠B=∠C. Prove that AE∣∣BC
View Solution
