In a circle of radius 7 cm, tangent PT is drawn from a point P such tht PT= 24 cm. If O is the centre of circle, then find the length of OP.
The correct Answer is:25cm
To find the length of OP in the given circle, we can follow these steps:
Step 1: Understand the Geometry
In the given problem, we have a circle with center O and radius 7 cm. A tangent PT is drawn from point P outside the circle, and the length of the tangent PT is given as 24 cm. The radius OP will be the hypotenuse of a right triangle formed by the radius OT (which is perpendicular to the tangent PT) and the tangent PT itself.
Step 2: Identify the Right Triangle
Since the radius (OT) is perpendicular to the tangent (PT) at point T, we can form a right triangle OPT where:
- OT = radius of the circle = 7 cm (one leg of the triangle)
- PT = length of the tangent = 24 cm (the other leg of the triangle)
- OP = length we need to find (the hypotenuse of the triangle)
Step 3: Apply the Pythagorean Theorem
According to the Pythagorean theorem, in a right triangle:
OP2=OT2+PT2
Substituting the known values:
OP2=72+242
OP2=49+576
OP2=625
Step 4: Solve for OP
Now, we take the square root of both sides to find OP:
OP=√625
OP=25cm
Conclusion
The length of OP is 25 cm.
---
In the given problem, we have a circle with center O and radius 7 cm. A tangent PT is drawn from point P outside the circle, and the length of the tangent PT is given as 24 cm. The radius OP will be the hypotenuse of a right triangle formed by the radius OT (which is perpendicular to the tangent PT) and the tangent PT itself.
Since the radius (OT) is perpendicular to the tangent (PT) at point T, we can form a right triangle OPT where:
- OT = radius of the circle = 7 cm (one leg of the triangle)
- PT = length of the tangent = 24 cm (the other leg of the triangle)
- OP = length we need to find (the hypotenuse of the triangle)
According to the Pythagorean theorem, in a right triangle:
OP2=OT2+PT2
OP2=72+242
OP2=49+576
OP2=625
Now, we take the square root of both sides to find OP:
OP=√625
OP=25cm
The length of OP is 25 cm.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Short Answer Questions4videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Long Answer Questions3videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Exercise25videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question5videos
ARITHMETIC PROGRESSION
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions9videos
CO-ORDINATE GEOMETRY
Similar Questions
In a circle of radius 7 cm, tangent PT is drawn from a point P such that PT=24 cm.If O is the center of circle then length OP=?
View SolutionA tangent is drawn from an external point O to a circle of radius 3 units at P such that OP = 4 units. If C is the centre of the circle, then the sine of the angle COP is
View Solution
Knowledge Check
- Question 1 - Select One
In Fig. 1, on a circle of radius 7 cm, tangent PT is drawn from a point P such that PT = 24 cm. If O is the centre of the circle, then the length of PR is
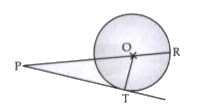 A30 cmB28 cmC32 cmD25 cm
A30 cmB28 cmC32 cmD25 cm - Question 2 - Select One
A tangent is drawn to a circle of radius 6 cm from a point situated at a distance of 10 cm from the centre of the circle the length of the tangent will be
A7cmB4cmC5cmD8cm - Question 3 - Select One
If the length of a tangent drawn from a point P to the circle is 24 cm and the distance of the point from the centre is 25 cm, then length of the radius is :
A12 cmB12.5 cmC1 cmD7 cm.
In the tangent of the circle. A tangent PT is drawn from an out side point P to the circle. If radius of circle is 5 cm and OP=13 cm then find the length of tangent PT.
 View Solution
View SolutionIf the angle between two tangents drawn from an external point ‘P’ to a circle of radius ‘r’ and centre O is 60∘, then find the length of OP.
View SolutionA point P is 13 xm from the centre of a circle . Radius of the circle is 5 cm . A tangent is drawn from point P to the circle , then the length of the tangent is :
View SolutionLength of a tangent segment drawn from a point which is at a distnace 12.5 cm from the centre of a circle is 12cm , find the diameter of the circle.
View SolutionIf the angle between two tangents drawn from an external point P to a circle of radius a and center O , is 60∘, then find the length of OP.
View Solution

