In a class test, the sum of Shefalis marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
To solve the problem step by step, let's denote Shefali's marks in Mathematics as m and her marks in English as e.
Step 1: Set up the equations
According to the problem, we have two conditions:
1. The sum of her marks in Mathematics and English is 30:
m+e=30
2. If she had got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210:
(m+2)(e−3)=210
Step 2: Express one variable in terms of the other
From the first equation, we can express e in terms of m:
e=30−m
Step 3: Substitute into the second equation
Now, substitute e in the second equation:
(m+2)((30−m)−3)=210
This simplifies to:
(m+2)(27−m)=210
Step 4: Expand the equation
Now, expand the left-hand side:
m⋅27−m2+2⋅27−2m=210
This simplifies to:
27m−m2+54−2m=210
Combining like terms gives:
25m−m2+54=210
Step 5: Rearrange the equation
Rearranging the equation gives:
−m2+25m+54−210=0
This simplifies to:
−m2+25m−156=0
Multiplying through by -1 to make the leading coefficient positive:
m2−25m+156=0
Step 6: Factor the quadratic equation
Now we need to factor the quadratic equation m2−25m+156=0. We are looking for two numbers that multiply to 156 and add to -25. The numbers are -12 and -13:
(m−12)(m−13)=0
Step 7: Solve for m
Setting each factor to zero gives us:
1. m−12=0 → m=12
2. m−13=0 → m=13
Step 8: Find corresponding e values
Now, we can find the corresponding values of e:
1. If m=12:
e=30−12=18
2. If m=13:
e=30−13=17
Final Answer
Thus, Shefali's marks in Mathematics and English can be:
1. m=12,e=18
2. m=13,e=17
According to the problem, we have two conditions:
1. The sum of her marks in Mathematics and English is 30:
m+e=30
2. If she had got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210:
(m+2)(e−3)=210
From the first equation, we can express e in terms of m:
e=30−m
Now, substitute e in the second equation:
(m+2)((30−m)−3)=210
This simplifies to:
(m+2)(27−m)=210
Now, expand the left-hand side:
m⋅27−m2+2⋅27−2m=210
This simplifies to:
27m−m2+54−2m=210
Combining like terms gives:
25m−m2+54=210
Rearranging the equation gives:
−m2+25m+54−210=0
This simplifies to:
−m2+25m−156=0
Multiplying through by -1 to make the leading coefficient positive:
m2−25m+156=0
Now we need to factor the quadratic equation m2−25m+156=0. We are looking for two numbers that multiply to 156 and add to -25. The numbers are -12 and -13:
(m−12)(m−13)=0
Setting each factor to zero gives us:
1. m−12=0 → m=12
2. m−13=0 → m=13
Now, we can find the corresponding values of e:
1. If m=12:
e=30−12=18
2. If m=13:
e=30−13=17
Thus, Shefali's marks in Mathematics and English can be:
1. m=12,e=18
2. m=13,e=17
Topper's Solved these Questions
Similar Questions
In a class test, the sum of the marks obtained by P in Mathematics and science is 28. Had he got 3 marks more in Mathematics and 4 marks less in Science. The product of his marks, would have been 180. Find his marks in the two subjects.
View SolutionRahul scores 80 marks in English and x marks in Hindi. What is his total score in the two subjects?
View Solution
Knowledge Check
- Question 1 - Select One
Rita scored 20 marks more in Maths than the marks scored in English. Give an expression for:
a. her marks in English if her marks in Maths are x.
b. her marks in Maths if her marks in English are y.Aa.20−x
b.y−20Ba.x+20
b.y+20Ca.x−20
b.y−20Da.x−20
b.y+20 - Question 2 - Select One
Raza scored 30 marks in Maths, x marks in Science and y marks in English. What is his total score in these three subjects ?
A30+x+yB30+x−yCx+y−30D30+30x+30y
The marks obtained by 10 candidates in English and Mathematics are given below:
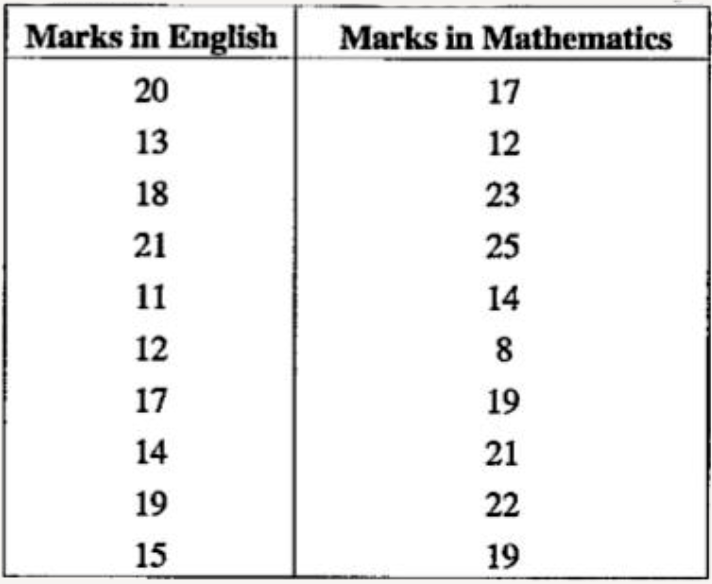
Estimate the probable score for Mathematics if the marks obtained in English are 24.View SolutionThe marks obtained in Mathematics and English are as follows. Calculate Spearman's Coefficient of rank correlations.
 View Solution
View SolutionThe score of Ishita in Mathematics is 25 more than the two third of her score in Science. If she scored x marks in Science, determine her score in Mathematics.
View SolutionThe marks obtained by 30 students of Class X of a certain school in a Mathematics paper consisting of 100 marks are presented in table below. Find the mean of the marks obtained by the students.
View SolutionSaina secure 70 marks in Science and 80 marks in Mathematics. Find
a. the ratio of Sania's marks in Science to her marks in Mathematics.
b. the ratio of Sania's marks in Mathematics to her marks is Science.View SolutionIn Figure, the pie-chart shows the marks obtained by a student in various subjects. If the student scored 135 marks in mathematics, find the total marks in all the subject. Also, find his score in individual subjects.
View Solution
