In a ΔABC,a,b,A are given and c1,c2 are two values of the third side c. The sum of the areas two triangles with sides a,b,c1anda,b,c2 is
12a2sin2A
12b2sin2A
b2sin2A
None of these
The correct Answer is:A
To solve the problem, we need to find the sum of the areas of two triangles with sides a,b,c1 and a,b,c2. We will use the sine formula for the area of a triangle, which states that the area A of a triangle with sides a and b and included angle A is given by:
Area=12absinA
1. Identify the Given Values:
We are given the sides a, b, and the angle A of triangle ABC. We also have two values for the third side c: c1 and c2.
2. Use the Sine Formula for Area:
The area of triangle ABC with sides a,b,c1 is given by:
Area1=12bc1sinA
The area of triangle ABC with sides a,b,c2 is given by:
Area2=12bc2sinA
3. Sum of the Areas:
The total area of both triangles is:
Total Area=Area1+Area2=12bc1sinA+12bc2sinA
Factoring out the common terms gives:
Total Area=12bsinA(c1+c2)
4. Using the Roots of the Quadratic Equation:
Since c1 and c2 are the roots of the quadratic equation derived from the cosine rule, we know:
c1+c2=2bcosA
Therefore, we can substitute this into the total area expression:
Total Area=12bsinA(2bcosA)
5. Simplifying the Expression:
This simplifies to:
Total Area=b2sinAcosA
6. Using the Double Angle Identity:
We can use the double angle identity for sine:
sin2A=2sinAcosA
Thus, we have:
Total Area=12b2sin2A
Final Result:
The sum of the areas of the two triangles is:
Total Area=12b2sin2A
We are given the sides a, b, and the angle A of triangle ABC. We also have two values for the third side c: c1 and c2.
The area of triangle ABC with sides a,b,c1 is given by:
Area1=12bc1sinA
The area of triangle ABC with sides a,b,c2 is given by:
Area2=12bc2sinA
The total area of both triangles is:
Total Area=Area1+Area2=12bc1sinA+12bc2sinA
Factoring out the common terms gives:
Total Area=12bsinA(c1+c2)
Since c1 and c2 are the roots of the quadratic equation derived from the cosine rule, we know:
c1+c2=2bcosA
Therefore, we can substitute this into the total area expression:
Total Area=12bsinA(2bcosA)
This simplifies to:
Total Area=b2sinAcosA
We can use the double angle identity for sine:
sin2A=2sinAcosA
Thus, we have:
Total Area=12b2sin2A
The sum of the areas of the two triangles is:
Total Area=12b2sin2A
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (More Than One Correct Option Type Questions)
23 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Statement I And Ii Type Questions)
11 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERSISE 1: SINGLE OPTION CORRECT TYPE QUESTIONS
1 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
In ΔABC,a,bandA are given and c1,c2 are two values of the third side c. Prove that the sum of the area of two triangles with sides a, b, c1anda,bc2 is 12b2sin2A
View SolutionIn a δABC, a,c, A are given and b1,b2 are two values of third side b such that b2=2b1. Then, the value of sin A.
View SolutionWhen any two sides and one of the opposite acute angle are given, under certain additional conditions two triangles are possible. The case when two triangles are possible is called the ambiguous case.
In fact when any two sides and the angle opposite to one of them are given either no triangle is posible or only one triangle is possible or two triangles are possible.
In the ambiguous case, let a,b and ∠A are given and c1,c2 are two values of the third side c.
On the basis of above information, answer the following questions
The value of c21−2c1c2cos2A+c22 is
View SolutionWhen any two sides and one of the opposite acute angle are given, under certain additional conditions two triangles are possible. The case when two triangles are possible is called the ambiguous case.
In fact when any two sides and the angle opposite to one of them are given either no triangle is posible or only one triangle is possible or two triangles are possible.
In the ambiguous case, let a,b and ∠A are given and c1,c2 are two values of the third side c.
On the basis of above information, answer the following questions
The difference between two values of c is
View SolutionIf in ΔABC, sides a, b, c are in A.P. then
View SolutionIf a, b and A are given in a triangle and c1,c2 are possible values of the third side, then prove that c21+c22−2c1c2cos2A=4a2cos2A
View SolutionIn a ΔABC, a, b, c are sides and A, B, C are angles opposite to them, then the value of the determinant
∣∣ ∣ ∣∣a2bsinAcsinAbsinA1cosAcsinAcosA1∣∣ ∣ ∣∣, is
View SolutionIf a,b,A be given in a triangle and c1andc2 be two possible value of the third side such that c21+c1c2+c22=a2, then a is equal to
View SolutionIn a triangle ABC,vertex angles A,B,C and side BC are given .The area of △ABC is
View SolutionIf A(2a,4a),B(2a,6a) are two vertices of a ΔABC then match the vertex C given by triangle
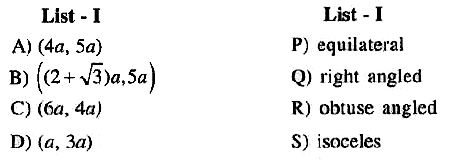
View Solution
