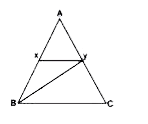
In a ΔABC, if the bisector of the angle BAC meets BC in D, then which one of the following is correct?
AB≤BD
∠DBA>12∠BAC
ΔABD can never be isosceles
If BD=AD, then ΔABD will be equilateral.
The correct Answer is:b
To solve the problem, we need to analyze the triangle ΔABC where the angle bisector of ∠BAC meets side BC at point D. We want to determine which statement about the angles in this triangle is correct.
1. Identify the Given Information:
- We have triangle ABC.
- The angle bisector AD of ∠BAC meets side BC at point D.
2. Understand the Angle Bisector:
- Since AD is the angle bisector, it divides ∠BAC into two equal parts:
∠DAC=∠DAB=12∠BAC
3. Consider the Exterior Angle:
- The exterior angle at vertex D (formed by extending side BC beyond point D) is given by:
∠BDA=∠DAB+∠ABC
- This means that ∠BDA is equal to the sum of ∠DAB and ∠ABC.
4. Apply the Exterior Angle Theorem:
- According to the exterior angle theorem, the exterior angle ∠BDA is greater than either of the opposite interior angles ∠DAC or ∠ABC:
∠BDA>∠DAC
5. Substituting the Values:
- Since ∠DAC=12∠BAC, we can express the relationship:
∠BDA>12∠BAC
6. Conclusion:
- Therefore, we can conclude that:
∠BDA>12∠BAC
- Among the options provided, the correct statement is that ∠BAD (which is equal to ∠DAB) is greater than 12∠BAC.
Final Answer:
The correct statement is that ∠BAD>12∠BAC.
- We have triangle ABC.
- The angle bisector AD of ∠BAC meets side BC at point D.
- Since AD is the angle bisector, it divides ∠BAC into two equal parts:
∠DAC=∠DAB=12∠BAC
- The exterior angle at vertex D (formed by extending side BC beyond point D) is given by:
∠BDA=∠DAB+∠ABC
- This means that ∠BDA is equal to the sum of ∠DAB and ∠ABC.
- According to the exterior angle theorem, the exterior angle ∠BDA is greater than either of the opposite interior angles ∠DAC or ∠ABC:
∠BDA>∠DAC
- Since ∠DAC=12∠BAC, we can express the relationship:
∠BDA>12∠BAC
- Therefore, we can conclude that:
∠BDA>12∠BAC
- Among the options provided, the correct statement is that ∠BAD (which is equal to ∠DAB) is greater than 12∠BAC.
The correct statement is that ∠BAD>12∠BAC.
Topper's Solved these Questions
- TRIANGLESBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - Question Bank- 18
24 Videos
- TRIANGLESBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - Self Assessment Sheet - 18
10 Videos
- TIME AND WORK BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TIME AND WORK EXERCISE - Self Assessment Sheet - 13
15 Videos
- VOLUME AND SURFACE AREA OF A CUBE AND A CUBOIDBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - VOLUME AND SURFACE AREA OF A CUBE AND A CUBOIDEXERCISE - UNIT TEST - 5
20 Videos
Similar Questions
Knowledge Check
In a triangle ABC, internal bisector of ∠ABC and external bisector of ∠ACB meet in D. Which one of the following is true ?
A∠BDC=∠BACB∠BDC=12∠ABCC∠BDC=∠DBCDNone of theseIf median of the ΔABC through A is perpendicular to BC, then which one of the following is correct ?
Atan A + tan B = 0Btan B - tan C = 0Ctan C + 2 tan A = 0Dtan B + tan C = 0
The median BD of the triangle ABC meets AC at D. If BD=12AC , then which one of the following is correct ?
View SolutionA(3,2,0),B(5,3,2) and C(−9,6,−3) are the vertices of a triangle ABC if bisector of angle BAC meets BC at D, then co-ordinates of D are
View SolutionThe side BC of a triangle ABC is produced to D, bisector of the angle ABC and ACD meet at P. If ∠BPC=x∘ and ∠BAC=y∘, then which one of the following is correct ?
View SolutionIn a triangle ABC, AD is perpendicular on BC. If ∠BAC=90∘,AB=c,BC=a,CA=b and AD = p, then which one of the following is correct?
View SolutionIn ΔABC, the bisector of the angle A meets the sides BC at D and the circumscirbed circle at E. Prove that DE=a2sec.A22(b+c)
View SolutionTriangle ABC as shown in the figure has line XY parallel to the BC and the line BY is the bisector of angle XYC . Which of the following option is correct ?
View Solution
