In a $Δ A B C, A = (2, 3)$ and medians through B and C have equations $x + y - 1 = 0$ and $2 y - 1 = 0$
Equation of side BC is (a) $5 x + 13 y + 11 = 0$ (b) $5 x - 3 y = 1$ (c) $5 x = 3 y$ (d) $5 x + 13 y - 11 = 0$

A

$5 x + 13 y + 11 = 0$

B

$5 x - 3 y = 1$

C

$5 x = 3 y$

D

$5 x + 13 y - 11 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

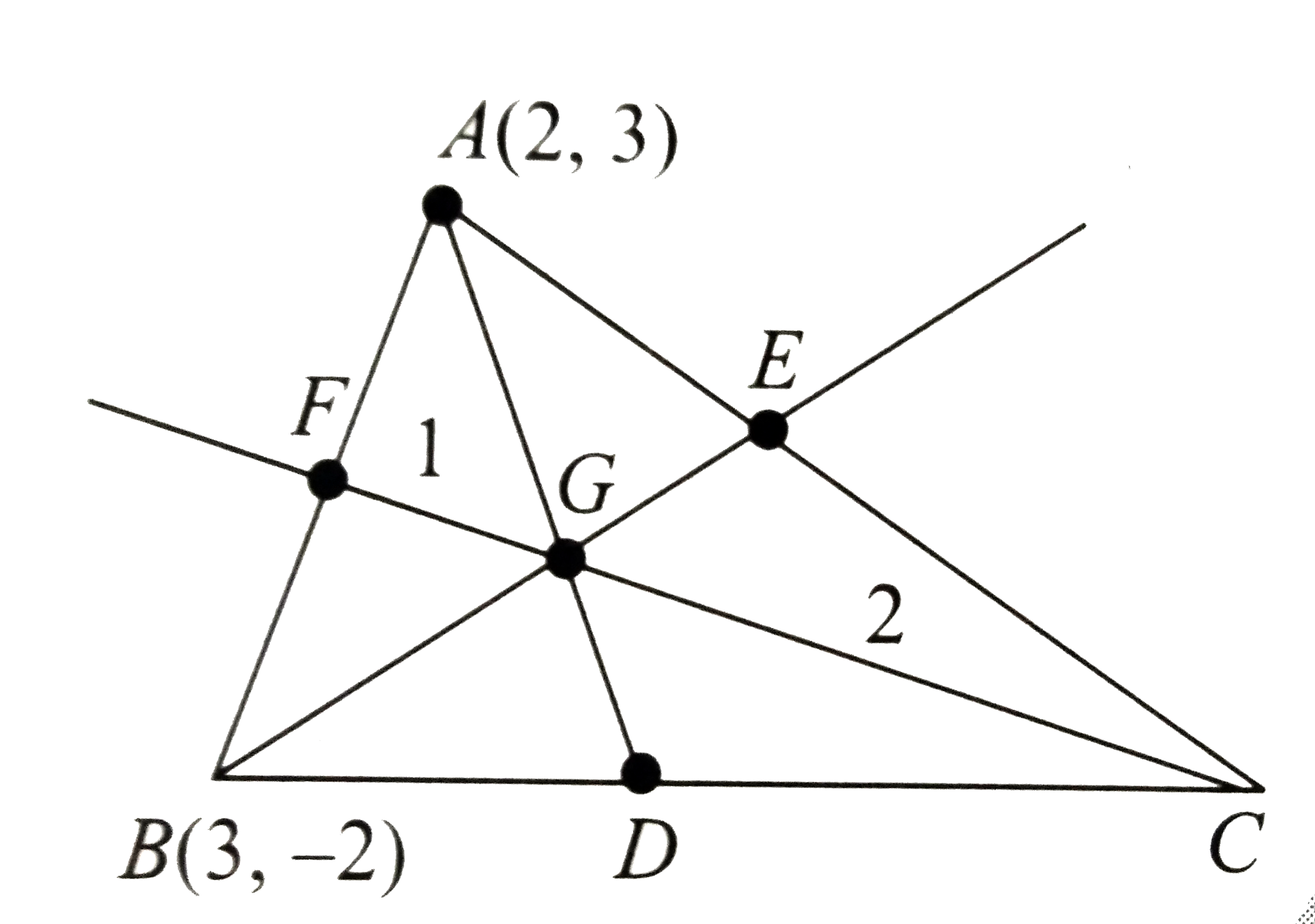
Centroid is the point of intersection of $x + y - 1 = 0, 2 y - 1 = 0$ or $D (\frac{1}{2}, \frac{1}{2})$
Slope of AD is $\frac{3 - \frac{1}{2}}{2 - \frac{1}{2}} = \frac{5}{3}$
$∴$ Equation of AD is $y - 3 = \frac{5}{3} (x - 2)$ or $5 x - 3 y - 1 = 0$
A point of $C F : 2 y - 1 = 0$ is $(α, \frac{1}{2})$
Let this be the midpoint of AB.
$∴$ B is $(2 α - 2, - 2)$ which lies on median $B E : x + y - 1 = 0$
$∴ 2 α - 2 - 2 - 1 = 0 ∴ α = \frac{5}{2}$
$∴ B (3, - 2)$
G divides CF in 2:1
$∴ C = (\frac{- 7}{2}, \frac{1}{2})$
$∴$ Equation of BC is $\frac{y + 2}{\frac{1}{2} + 2} = \frac{x - 3}{\frac{- 7}{2} - 3}$
or $\frac{y + 2}{5} = \frac{x - 3}{- 13}$
or $5 x + 13 y + 11 = 0$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINE

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-STRAIGHT LINE-Comprehension Type

Home
Ask Doubt
Profile