Question

In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4, French and Sanskrit = 5, English , French and Sanskrit = 3. Find the number of students who study
(i) only French, (ii) only English.
(iii) only Sanskrit. ,
(iv) atleast one of the three languages.
(v) none of the three languages.

Explanation

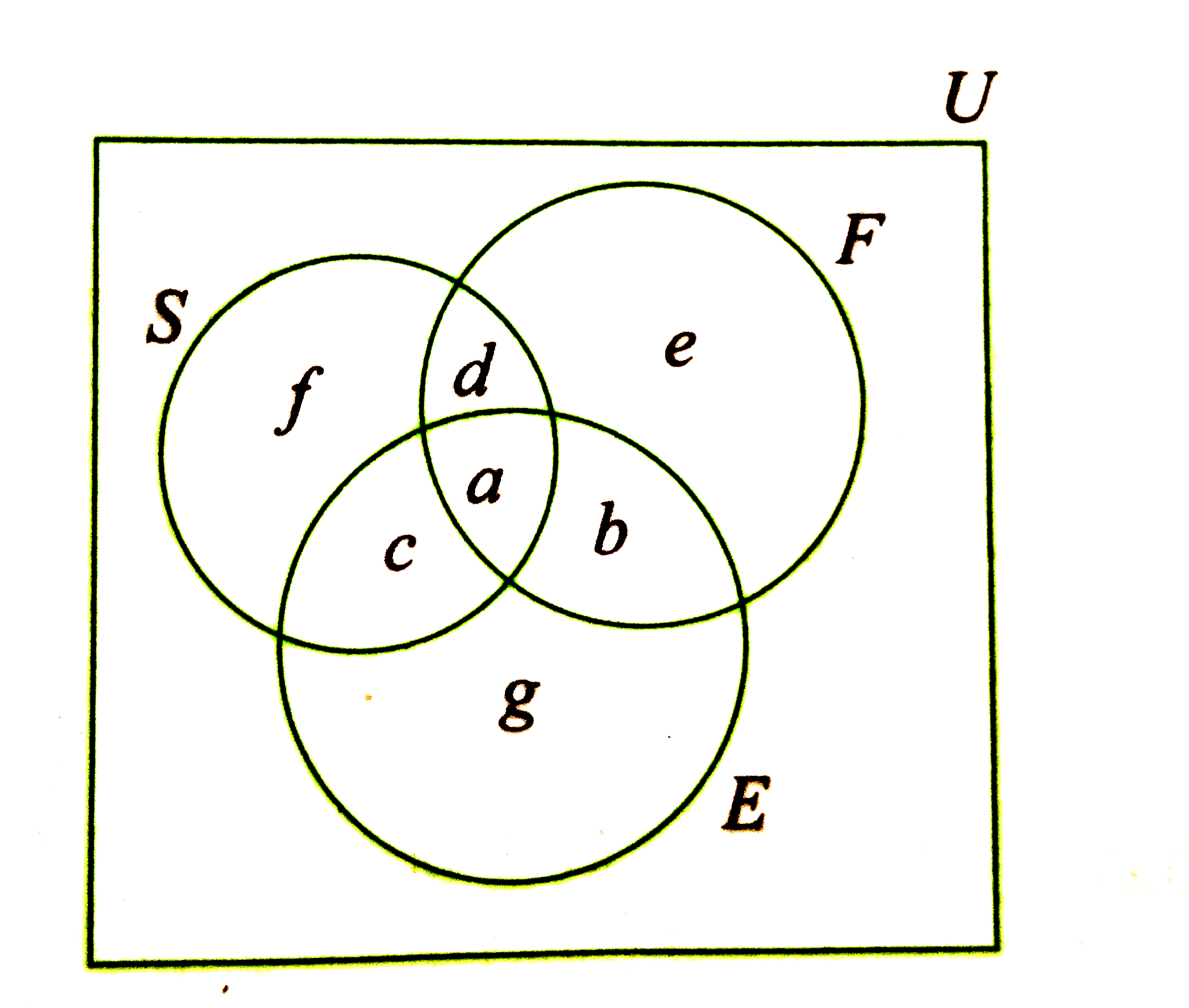
Let pet F, E and S be the sets of students whole arn French, English ,md Sanskrit, respectively. Then,` n(U) = 50, n(F) = 17, n(E)=13, n(S) = 15, n(F cap E)=9,n(E cap S)=4,n(F cap S)=5," and " n(F cap E cap S)=3`. From the figure, we have
`a= n ( E cap F cap S )=3 and a+d =n ( F cap S) = 5 rArr d= 2 `
`a + b =n ( F cap E )= 9 rArr b=6 `
`a+ c =n ( F cap S )=4 rArr c= 1`
`a+b+d+e = n ( F) = 17 rArr 3+ 6+ 2+ e= 17 rArr e= 6`
`a+b+c+g = n ( F) = 13 rArr 3+6+1+g= 13 rArr g=3`
`a+c+d+f =n (S) = 15 rArr 3+1+2+f = 15 rArr f=9 `
Number of student learining French only = e = 6
(ii) Number of students learning English only = g = 3
(iii) Number of students learning Sanskrit only = f = 9
(iv) Number of students learning English and Sanskrit but not French = c = 1
(v) Number of students learning French and Sanskrit but not English = d = 2
(vi) Number of students learning F rench and English but not Sanskrit = b = 6
(vii) Number of students learning at least one of the three languages=a+b+c+d+e+f+g=30
(viii) Number of students learning none of the three languages = 50 - 30 = 20 .
(ix) Number of students learning exactly one language =e+f+g=6+3+9=18
(x) Number of students learning exactly two languages =b+c+d=6+2+l=9