In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?
To solve the problem step by step, we will use the information given about the group of people who like cricket and tennis.
Step 1: Identify the given information
- Total number of people = 65
- Number of people who like cricket = 40
- Number of people who like both cricket and tennis = 10
Step 2: Determine the number of people who like only cricket
To find the number of people who like only cricket, we subtract the number of people who like both cricket and tennis from the total number of cricket lovers.
Number of people who like only cricket=Number of cricket lovers−Number of people who like both
=40−10=30
Step 3: Determine the number of people who like tennis only
Let’s denote the number of people who like tennis as T. The number of people who like tennis only can be found by subtracting the number of people who like both from the total number of tennis lovers.
To find the total number of people who like tennis, we can use the information about the total number of people in the group.
Total people=People who like only cricket+People who like only tennis+People who like both
Let x be the number of people who like only tennis. Then we have:
65=30+x+10
Step 4: Solve for x
Now, we can simplify the equation to find x:
65=40+x
x=65−40=25
So, the number of people who like tennis only is 25.
Step 5: Calculate the total number of people who like tennis
Now that we know how many people like tennis only, we can find the total number of people who like tennis:
Total number of people who like tennis=People who like only tennis+People who like both
=25+10=35
Final Answers
- Number of people who like tennis only: 25
- Total number of people who like tennis: 35
- Total number of people = 65
- Number of people who like cricket = 40
- Number of people who like both cricket and tennis = 10
To find the number of people who like only cricket, we subtract the number of people who like both cricket and tennis from the total number of cricket lovers.
=40−10=30
Let’s denote the number of people who like tennis as T. The number of people who like tennis only can be found by subtracting the number of people who like both from the total number of tennis lovers.
Let x be the number of people who like only tennis. Then we have:
Now, we can simplify the equation to find x:
x=65−40=25
Now that we know how many people like tennis only, we can find the total number of people who like tennis:
=25+10=35
- Number of people who like tennis only: 25
- Total number of people who like tennis: 35
Topper's Solved these Questions
- SETSBOOK - NCERTCHAPTER - SETSEXERCISE - EXERCISE 1.4
12 Videos
- SETSBOOK - NCERTCHAPTER - SETSEXERCISE - EXERCISE 1.5
7 Videos
- SETSBOOK - NCERTCHAPTER - SETSEXERCISE - SOLVED EXAMPLES
30 Videos
- SEQUENCES AND SERIESBOOK - NCERTCHAPTER - SEQUENCES AND SERIESEXERCISE - EXERCISE 9.5
6 Videos
- STATISTICSBOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 15.2
10 Videos
Similar Questions
In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?
View SolutionIn a group of 100 people, 60 people like to play cricket, 20 people like to play both cricket and Tennis. How many people like to play Tennis but not cricket?
View Solution
Knowledge Check
In a group of 60 persons, 40 persons like play cricket and 10 persons like play both Tennis and Cricket. Then, the number of persons who like to play Tennis, is
A20B25C30D40In a group of 60 persons, 40 persons like play cricket and 10 persons like play both Tennis and Cricket. Then, the number of persons who like to play Tennis, is
A20B25C30D40
In a group of 70 people, 37 like coffee, 52 like tea and each person likes at least one of the two drinks. How many people like both coffee and tea?
View SolutionIn a survey of 450 people, it was found that 110 play cricket, 160 play tennis and 70 play both cricket as well as tennis. How many play neither cricket nor tennis?
View SolutionIn the given figure, how many people like cricket and tennis both ?
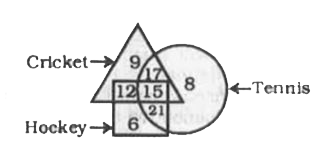
View SolutionIn a group of 50 people , 30 like to play cricket , 25 like to play football and 32 like play hockey . Assume that each one like to play atleast one of the three games . If 15 people like to play both cricket as well as football, 11 people like to play both football well as hockey and 18 like to play both football as as hockey, then
(i) how many like to play all the three games?
(ii) how many like to play only football ?
(iii) how many like to play only hockey ?
View SolutionIn a group of 36 students, 18 like volleyball, 12 like hockey, and 14 like neither of the games. How many like both games?
View SolutionIn a group of 200 students, 20 played cricket only, 36 plated tennis only, 40 played, hockey only, 8 played cricket and tennis, 20 played cricket and hockey, 28 played hockey and tennis and 80 played hockey. By Venn diagram, find the number of students who (i) played cricket (ii) played tennis (iii) did not played any of the above three games.
View Solution
