In a hurdle race, a runner has probability p of jumping over a specific hurdle. Given that in 5 trials, the runner succeeded 3 times, the conditional probabilit that the runner had succeeded in the first trial is
3/5
2/5
1/5
None of these
The correct Answer is:A
(a) Let A denote the event that the runner succeeds exactly 3 times out of five and B denote the events that the runner suceeds on the first trial.
P(B/A)=P(B∩A)P(A)
But P(B∩A)=P (clearing succeeding in the first trial and exactly once in two other trials)
=4C2p2(1−p)2)=6p3(1−p)2
and P(A)=5C3p3(1−p)2=10p3(1−p)2
Thus, P(B/A)=6p3(1−p)210p3(1−p)2=35
Topper's Solved these Questions
- PROBABILITYBOOK - CENGAGECHAPTER - PROBABILITYEXERCISE - Multiple Correct Answer
13 Videos
- PROBABILITYBOOK - CENGAGECHAPTER - PROBABILITYEXERCISE - Comprehension
2 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTIONBOOK - CENGAGECHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Exercise
9 Videos
- PROBABILITY AND STATISTICSBOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank
37 Videos
Similar Questions
Read the following extract and answer the questions given below :
The special school did Chaitanya a lot of good. He was now a much more confident person, adored by his teachers, his friends and his school satff.His speech improved and expression became clearer. His social manners became laudable.
Academically, he was still lagging behind the expected standard of learing, but it was okay. He started developing an all -round interset in carft, art, music, dancing and sprots.
Early in 1997-98, when he returned form state level inter-school, sports , he had tow prizes to his credit and a silver medal. He has won his laurels in athletic events and the silver medal in a running race.
When I saw the prizes and read he citation Chaitanya had recevied , I was stupefied, in total disbelief , then - hugged him, kissed him and cried unabashedly to my heart's countent . That day, I cried for the first time out of joy and a sence of being vindicated. Without parctice he had competed with approximately 1,800 children draw form various schools all over the state . He was subsequently selected for the marathon race, but he could not participate due to health problem. '' May be next year, he would proudly chronicle his future achievements and success to inspire other mothers of the world.
Looking back at my own life , I feel that it is the spirit with which we can accept our life gracefully is what matters ultimately , and it is love which nourishes us .
Rewrite the following sentences in the ways instructed :
He was still lagging behind the expected standard of learing , but it was okay.
(Rewrite the sentence using 'Although').
View SolutionRead the following extract and answer the questions given below :
The special school did Chaitanya a lot of good. He was now a much more confident person, adored by his teachers, his friends and his school satff.His speech improved and expression became clearer. His social manners became laudable.
Academically, he was still lagging behind the expected standard of learing, but it was okay. He started developing an all -round interset in carft, art, music, dancing and sprots.
Early in 1997-98, when he returned form state level inter-school, sports , he had tow prizes to his credit and a silver medal. He has won his laurels in athletic events and the silver medal in a running race.
When I saw the prizes and read he citation Chaitanya had recevied , I was stupefied, in total disbelief , then - hugged him, kissed him and cried unabashedly to my heart's countent . That day, I cried for the first time out of joy and a sence of being vindicated. Without parctice he had competed with approximately 1,800 children draw form various schools all over the state . He was subsequently selected for the marathon race, but he could not participate due to health problem. '' May be next year, he would proudly chronicle his future achievements and success to inspire other mothers of the world.
Looking back at my own life , I feel that it is the spirit with which we can accept our life gracefully is what matters ultimately , and it is love which nourishes us.
Rewrite the following sentences in the ways instructed:
He started developing an all-round intereset in carft and sports.
(Rewrite the sentence using infinitive form of the word underlined).
View Solution
Knowledge Check
In a hurdle race, a runner has probability p of jumping over a specific hurdle. Given that in 5 trials, the runner succeeded 3 times, the conditionals probability that the runner had succeeded in the first trial, is
A35B25C15DNone of theseIn a hurdle race, a runner has probability p of jumping over a specific hurdle. Given that in 5 trials, the runner succeeded 3 times, the conditional probabilit that the runner had succeeded in the first trial is
A35B25C15DNoneA biased coin is tossed repeatedly until a tail appears for the first time. Heads is 3 times as likely to appear as tails. Let x be the number of tosses required. Assume that all the trials of tossing a biased coin are independent. Then, the conditional probability that x≥6, gives that x>3, is equal to
A916B116C12D35
Read the following extract and answer the questions given below :
The special school did Chaitanya a lot of good. He was now a much more confident person, adored by his teachers, his friends and his school satff.His speech improved and expression became clearer. His social manners became laudable.
Academically, he was still lagging behind the expected standard of learing, but it was okay. He started developing an all -round interset in carft, art, music, dancing and sprots.
Early in 1997-98, when he returned form state level inter-school, sports , he had tow prizes to his credit and a silver medal. He has won his laurels in athletic events and the silver medal in a running race.
When I saw the prizes and read he citation Chaitanya had recevied , I was stupefied, in total disbelief , then - hugged him, kissed him and cried unabashedly to my heart's countent . That day, I cried for the first time out of joy and a sence of being vindicated. Without parctice he had competed with approximately 1,800 children draw form various schools all over the state . He was subsequently selected for the marathon race, but he could not participate due to health problem. '' May be next year, he would proudly chronicle his future achievements and success to inspire other mothers of the world.
Looking back at my own life , I feel that it is the spirit with which we can accept our life gracefully is what matters ultimately , and it is love which nourishes us .
Rewrite the followong sentence in the ways instructed:
Rewrite the following sentence in the ways instructed:
(i) When I saw the prices , I was stupefied.
(Rewrite the sentence using 'No sonner……… than).
View SolutionA biased coin with probability p(0<p<1) of falling tails is tossed until a tail appears for the first time. If the probability that tail comes in odd number of trials is 23, then p equals
View SolutionIn a series of n independent trials for an event of consist probability p, the most probable number r of successes is given by (n+1)p−1<r<(n+1)p.
Hence the most probable number of successes is the integral part of (n+1) p, But if (n+1) p is an integer the chance of r successes is equal to that of (r+1) successes and bot r,r+1 are most problem number of successes.
A bag contains 2 white and 1 black balls. A ball is drawn at random and returned to bag.
The experiment is done 10 times. The probability that a white ball is drawn exactly 5 times is .
View SolutionIn a series of n independent trials for an event of consist probability p, the most probable number r of successes is given by (n+1)p−1<r<(n+1)p.
Hence the most probable number of successes is the integral part of (n+1) p, But if (n+1) p is an integer the chance of r successes is equal to that of (r+1) successes and bot r,r+1 are most problem number of successes.
A bag contains 2 white and 1 black balls. A ball is drawn at random and returned to bag.
The experiment id done 5 times. The probability that a white ball is drawn most of the time is.
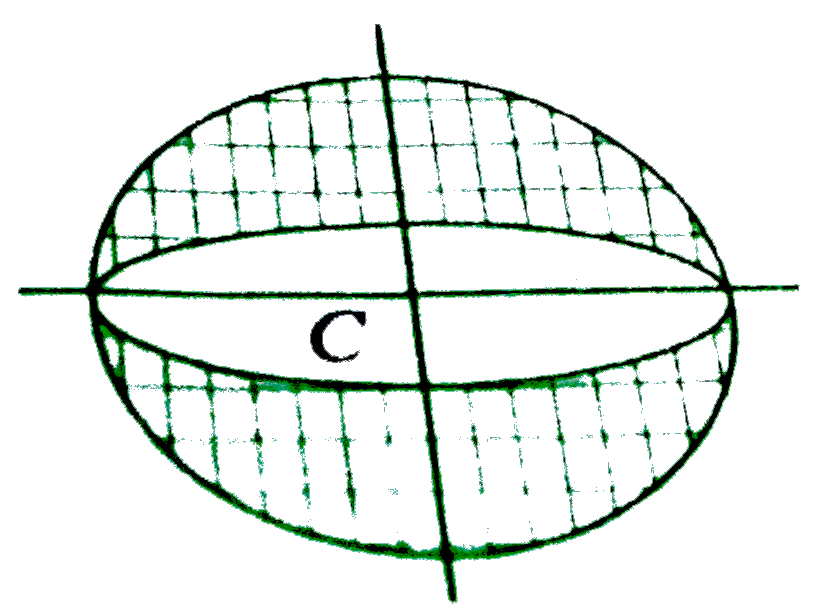
View SolutionThere are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity 2√2/3 is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
1−b2a2=89orb2a2=19
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
p=Area of shaded regionArea of circle
=πa2−πabπa2=1−ba=1−13=23
Now, answer the following questions.
Two persons A and B agree to meet at a place between 5 and 6 pm. The first one to arrive waits for 20 min and then leave. If the time of their arrival be independant and at random, then the probability that A and B meet is
View Solution
