In a magic square each row, column and diagonal have the same sum. Check if the figure is a magic square.
To determine if the given figure is a magic square, we need to check if the sums of all rows, columns, and diagonals are the same. Let's go through the steps systematically.
Step 1: Identify the Rows
Assuming the magic square is represented as follows:
Row1:1−100Row2:−4−3−2Row3:−64−7
Step 2: Calculate the Sum of Each Row
- Sum of Row 1:
\(
1 + (-10) + 0 = 1 - 10 + 0 = -9
\)
- Sum of Row 2:
\(
-4 + (-3) + (-2) = -4 - 3 - 2 = -9
\)
- Sum of Row 3:
\(
-6 + 4 + (-7) = -6 + 4 - 7 = -9
\)
Step 3: Identify the Columns
Now, let's calculate the sums for each column.
- Column 1:
\(
1 + (-4) + (-6) = 1 - 4 - 6 = -9
\)
- Column 2:
\(
-10 + (-3) + 4 = -10 - 3 + 4 = -9
\)
- Column 3:
\(
0 + (-2) + (-7) = 0 - 2 - 7 = -9
\)
Step 4: Calculate the Sums of the Diagonals
Next, we will check the diagonals.
- Diagonal 1 (from top left to bottom right):
\(
1 + (-3) + (-7) = 1 - 3 - 7 = -9
\)
- Diagonal 2 (from top right to bottom left):
\(
0 + (-3) + (-6) = 0 - 3 - 6 = -9
\)
Step 5: Conclusion
After calculating the sums, we find:
- Sum of Row 1 = -9
- Sum of Row 2 = -9
- Sum of Row 3 = -9
- Sum of Column 1 = -9
- Sum of Column 2 = -9
- Sum of Column 3 = -9
- Sum of Diagonal 1 = -9
- Sum of Diagonal 2 = -9
Since all the sums are equal to -9, we conclude that the figure is indeed a magic square.
Final Answer
Yes, the figure is a magic square.
---
Assuming the magic square is represented as follows:
- Sum of Row 1:
\(
1 + (-10) + 0 = 1 - 10 + 0 = -9
\)
- Sum of Row 2:
\(
-4 + (-3) + (-2) = -4 - 3 - 2 = -9
\)
\(
-6 + 4 + (-7) = -6 + 4 - 7 = -9
\)
Now, let's calculate the sums for each column.
\(
1 + (-4) + (-6) = 1 - 4 - 6 = -9
\)
\(
-10 + (-3) + 4 = -10 - 3 + 4 = -9
\)
\(
0 + (-2) + (-7) = 0 - 2 - 7 = -9
\)
Next, we will check the diagonals.
\(
1 + (-3) + (-7) = 1 - 3 - 7 = -9
\)
\(
0 + (-3) + (-6) = 0 - 3 - 6 = -9
\)
After calculating the sums, we find:
- Sum of Row 1 = -9
- Sum of Row 2 = -9
- Sum of Row 3 = -9
- Sum of Column 1 = -9
- Sum of Column 2 = -9
- Sum of Column 3 = -9
- Sum of Diagonal 1 = -9
- Sum of Diagonal 2 = -9
Yes, the figure is a magic square.
Topper's Solved these Questions
- INTEGERSBOOK - NCERT ENGLISHCHAPTER - INTEGERSEXERCISE - EXERCISE 1.4
7 Videos
- INTEGERSBOOK - NCERT ENGLISHCHAPTER - INTEGERSEXERCISE - EXERCISE 1.2
4 Videos
- FRACTIONS AND DECIMALSBOOK - NCERT ENGLISHCHAPTER - FRACTIONS AND DECIMALSEXERCISE - EXERCISE 2.7
6 Videos
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - EXERCISE 5.2
6 Videos
Similar Questions
A magic square is an array of numbers having the same number of rows and columns and the sum of the numbers in a row column and the sum of the numbers in each row column or diagonal being the same. Fill in the blank cells of the following magic square.
View SolutionEXAMPLE 3 A magic square is an array of numbers having the same number of rows and columns and the sum of the numbers in a row column and the sum of the numbers in each row column or diagonal being the same. Fill in the blank cells of the following magic square.
View SolutionIn a “magic square”, the sum of the numbers in each row, in each column and along the diagonal is the same. Is this a magic square?
View SolutionIn a 4×4 matrix the sum of each row, column and both the main diagonals is α. Then the sum of the four corner elements
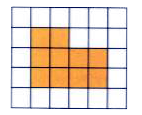
View SolutionCalculate the area of the figure if each square is 1cm2
View SolutionFind the square of 87 by using column method and diagonal method.
View SolutionA grid is made up of 13 rows of squares , each having 14 identical squares, Bolo comes and wants to draw some more square to the girl. So , he draw 3 additional rows and add 'S' additional squares in each row, including the ones he added himself . Which of the following expression correctly represents the increase in the total number of squares in the grid ?
View SolutionThe square of the diagonal of a square is 50 sq. units. Find the side of the square.
View SolutionIf (a, b) be an end of a diagonal of a square and the other diagonal has the equation x−y=a, then another vertex of the square can be
View SolutionA square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
View Solution
