Question

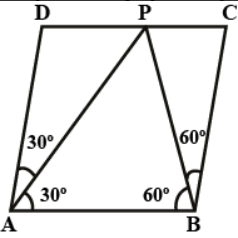
In a parallelogram ${\displaystyle ABCD, AB=10cm, AD=6cm\stackrel{.}{}}$
The bisector of ${\displaystyle \angle A}$
meets ${\displaystyle DC}$
in ${\displaystyle E, AE and BC}$
produced meet at ${\displaystyle F\stackrel{.}{}}$
Find the length C Foot

Explanation

It is given that `ABCD` is a parallelogram,
in which `AB=10 cm` and `AD=6 cm`.
the bisector of `angle A` mets `DC` in `E`.
`AE` and `BC` produce meet at `F`.
From the figure we have ,
`angle BAE=angle EAD........(1) [:'bisect of angle A]`
`angle EAD=angle EFB.......(2) [alternate angle S]`
therefore ,from `(1)` and `(2)`,we obtain
`angle BAE=angle EFB`
`:.BF=AB ` [`:'`side opposite to equal angle `S` are equal]
`implies BF=10cm [:'AB=10cm]`
`implies BC+CF=10cm`
`implies 6cm +CF=10cm` [`:'BC=AD=6cm`,opposite sides of parallelogram]
`implies CF=10-6=4cm`.
therefore we get required result.