In a parallelogram
the diagonals bisect each other at
If
Find:
Given that
[We know that measure of opposite angles are equal in a parallelogram]
(alternate angles)
[we know, opposite angles are equal in a parallelogram]
[we know, Alternate interior angles are equal]
In
[since, sum of all angles of a triangle is 180^0]
(opposite angle of the parallelogram)
In
[since, sum of all angles of a triangle is 180^0]
Video Solution
Text Solution
Given that
[We know that measure of opposite angles are equal in a parallelogram]
∠BDA = ∠ADB = ∠ADC – ∠BDC 30^2 – 10^2 = 20^2∠DAB = 180^0 – 30^0 = 150^0 ∠ADB = ∠DBC = 20^0 ∠BCD = ∠DAB = 150^0 ∠DBA = ∠BDC = 10^0 ΔABC∠CAB + ∠ABC + ∠BCA = 180^070^0 + 30^0 + ∠BCA = 180^0∠BCA = 180^0 – 100^0 = 80^0 ∠DAB = ∠DAC + ∠CAB = 70^0 + 80^0 = 150^0 ∠BCD = 150^0 ∠DCA = ∠CAB = 70^0 ΔDOC ∠BDC + ∠ACD + ∠DOC = 180^010^0 + 70^0 + ∠DOC = 180^0 ∠DOC = 180^0- 80^0∠ACB = 80^0
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a quadrilateral ABCD, the bisectors of ∠A and ∠B meet at O. If ∠C=70∘and∠D=130∘, then measure of ∠AOBis
A40∘B60∘C80∘D100∘
In a parallelogram ABCD, if ∠D=115∘, then write the measure of ∠A
View SolutionABCD is a cyclic quadrilateral in which: BCAD, ∠ADC=1100 and ∠BAC=500. Find ∠DAC ∠DBC=800 and ∠BAC=400. Find ∠BCD ∠BCD=1000and ∠ABD=700 find ∠ADB
View SolutionIn a parallelogram ABCD, if ∠A=(3x−20)∘,∠B=(y+15)∘,∠C=(x+40)∘, then find the values of xandy
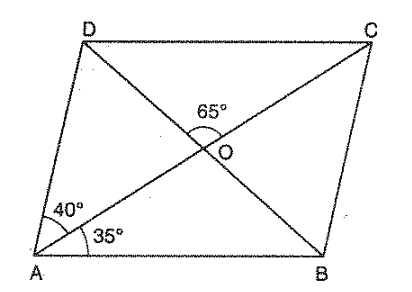
View SolutionIn Figure, ABCD is a parallelogram in which ∠DAO=400, ∠BAO=350 and ∠COD=650. Find: ∠ABO (ii) ∠ODC (iii) ∠ACB (iv) ∠CBD
View SolutionIn Fig.81, side BC of ABC has been produced to D and CEBA. If ∠ABC=650, ∠BAC=550, find ∠ACE, ∠ECD and ∠ACD.
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8 cm and BD=5.6cm . Find the measures of OC and OD
View Solution
