In a potato race 20 potatoes are placed in a line at intervals of 4meters with first potato 24metres from the starting point. A contestant is required to bring the potatoes back to the starting place one at a time. How far would he run in bringing back all the potatoes?
To solve the problem step by step, we will calculate the total distance the contestant runs to bring back all the potatoes.
Step 1: Understand the Position of the Potatoes
The first potato is placed at a distance of 24 meters from the starting point, and each subsequent potato is placed at intervals of 4 meters.
Step 2: Determine the Distances of Each Potato
The distance of each potato from the starting point can be expressed as follows:
- Distance of the 1st potato (a1) = 24 meters
- Distance of the 2nd potato (a2) = 24 + 4 = 28 meters
- Distance of the 3rd potato (a3) = 24 + 2*4 = 32 meters
- ...
- Distance of the nth potato (an) = 24 + (n-1)*4
Since there are 20 potatoes, we can find the distance of the 20th potato:
- Distance of the 20th potato (a20) = 24 + (20-1)*4 = 24 + 76 = 100 meters
Step 3: Calculate the Total Distance for Each Potato
The contestant runs to each potato and brings it back to the starting point. Therefore, the distance traveled for each potato is twice the distance to the potato:
- Distance for the 1st potato = 2 * 24 = 48 meters
- Distance for the 2nd potato = 2 * 28 = 56 meters
- Distance for the 3rd potato = 2 * 32 = 64 meters
- ...
- Distance for the nth potato = 2 * (24 + (n-1)*4)
Step 4: Formulate the Series
The distances traveled for the potatoes can be represented as:
- a1 = 48 meters
- a2 = 56 meters
- a3 = 64 meters
- ...
- a20 = 200 meters
This forms an arithmetic progression (AP) where:
- First term (a) = 48 meters
- Common difference (d) = 8 meters (since each subsequent distance increases by 8 meters)
Step 5: Use the Sum Formula for Arithmetic Progression
The formula for the sum of the first n terms of an arithmetic progression is:
Sn=n2×(2a+(n−1)d)
Where:
- n = number of terms (20 potatoes)
- a = first term (48 meters)
- d = common difference (8 meters)
Step 6: Substitute Values into the Formula
Substituting the values into the formula:
S20=202×(2×48+(20−1)×8)
S20=10×(96+152)
S20=10×248
S20=2480 meters
Conclusion
The total distance the contestant would run in bringing back all the potatoes is 2480 meters.
---
The first potato is placed at a distance of 24 meters from the starting point, and each subsequent potato is placed at intervals of 4 meters.
The distance of each potato from the starting point can be expressed as follows:
- Distance of the 1st potato (a1) = 24 meters
- Distance of the 2nd potato (a2) = 24 + 4 = 28 meters
- Distance of the 3rd potato (a3) = 24 + 2*4 = 32 meters
- ...
- Distance of the nth potato (an) = 24 + (n-1)*4
- Distance of the 20th potato (a20) = 24 + (20-1)*4 = 24 + 76 = 100 meters
The contestant runs to each potato and brings it back to the starting point. Therefore, the distance traveled for each potato is twice the distance to the potato:
- Distance for the 1st potato = 2 * 24 = 48 meters
- Distance for the 2nd potato = 2 * 28 = 56 meters
- Distance for the 3rd potato = 2 * 32 = 64 meters
- ...
- Distance for the nth potato = 2 * (24 + (n-1)*4)
The distances traveled for the potatoes can be represented as:
- a1 = 48 meters
- a2 = 56 meters
- a3 = 64 meters
- ...
- a20 = 200 meters
- First term (a) = 48 meters
- Common difference (d) = 8 meters (since each subsequent distance increases by 8 meters)
The formula for the sum of the first n terms of an arithmetic progression is:
Sn=n2×(2a+(n−1)d)
Where:
- n = number of terms (20 potatoes)
- a = first term (48 meters)
- d = common difference (8 meters)
Substituting the values into the formula:
S20=202×(2×48+(20−1)×8)
S20=10×(96+152)
S20=10×248
S20=2480 meters
The total distance the contestant would run in bringing back all the potatoes is 2480 meters.
Topper's Solved these Questions
Similar Questions
In a potato race 20 potatoes are placed in a line at intervals of 4meters with first potato 24metres from the starting point. A constant is required to bring the potatoes back to the starting place one at a time. How far would he run in bringing back all the potatoes?
View SolutionIn a potato race, a bucket is placed at the starting point, which is 7 meter from the first potato. The other potatoes are placed 4 m a part in a straight line from the first one. There are n potatoes in the line. Each competitor starts from the bucket, picks up the nearest potato, runs back with it, drops in the bucket, runs back to pick up the next potato, runs to the bucket and drops it and this process continues till all the potatoes are picked up and dropped in the bucket. Each competitor ran a total of 150 m. The number of potatoes is.____________
View SolutionIn a potato race, a bucket is placed at the starting point, which is 5 m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see Figure).A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?[Hint : To pick up the first potato and the second potato, the total distance (in metres) rim by a competitor is 2 x 5 + 2 x (5 + 3)]
 View Solution
View SolutionIn a potato race, a bucket is placed at the starting point, which is 5 m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see Figure). A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run? [Hint : To pick up the first potato and the second potato, the total distance (in metres) rim by a competitor is 2 x 5 + 2 x (5 + 3)]
View SolutionA 20 H inductor is placed in series with 10 W resistor and an emf of 100 V is suddenly applied to the combination. At t = 1 s from t = 1 s from the start, find the rate at which energy is being stored in the magnetic field around the inductor (givne e−0.5=0.61).
View SolutionA sound source S, emitting a sound of frequency 400 Hz and a receiver R of mass m are at the same point. R is performing SHM with the help of a spring of force constant K. At a time t = 0, R is at the mean position and moving towards the right, as shown. At the same time, the source starts moving away from R with some acceleration a. The frequency registered by the receiver at a time t = 10 s is 250 Hz. What is the time (in seconds) at which the corresponding registered frequency of 250 Hz was emitted by the source? [Given that mK=25π2 and amplitude of oscillation = 100πm,Vsound = 320 m s^(-1)]
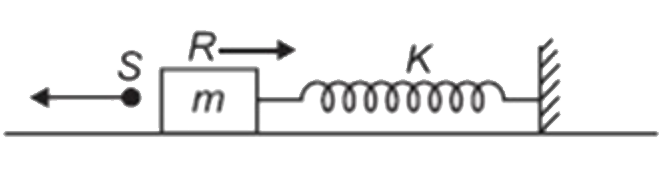 View Solution
View SolutionA rectangular frame of wire is placed in a uniform magnetic field directed outwards , normal to the paper . AB is connected to a spring which is stretched to A'B' and then released at time t=0. Explain qualitatively how induced e. m .f in the coil would very with time . (Neglect damping of oscillations of spring).
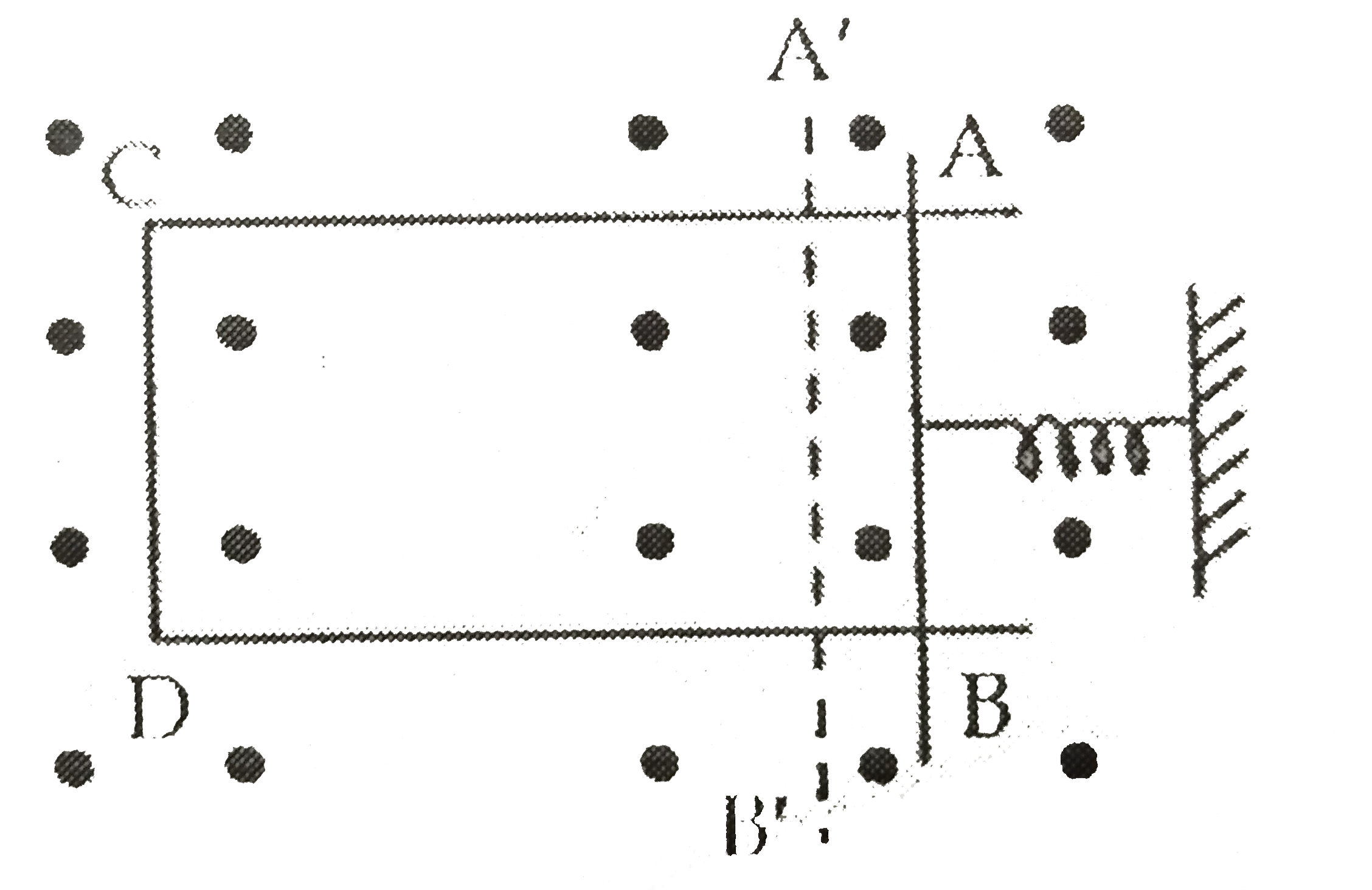 View Solution
View SolutionA river flows due south with a speed of 2.0ms−1. A man strees a motorboat across the river , his velocity relative to the water is 4ms−1 due east. The river is 800m wide.
(a) What is his velocity (magnitude and direction) relative to the earth ?
(b) How much time is required to cross the river ?
( c) HOw far south of his starting points will he reach the opposite bank ?View SolutionThe cost of papering four walls of a room at 70 paise per square meter is Rs.157.50. The height of the room is 5 metres. Find the length and the breadth of the room if they are in the ratio 4:1
View SolutionThe length and bredth of a hall are in the ratio 4:3 and its height is 5.5metres. The cost of decorating its walls (including doors and windows) at Rs.6.60persquaremetre is Rs.5082. Find the length and breadth of the room.
View Solution

