In a right angle, the sides conrtaining right angles are 5 cm and 12 cm. It is rotated aboutits hypotenuse taking it as axis. Find the total surface area and volume of formed figure.

Video Solution

Text Solution

Verified by Experts

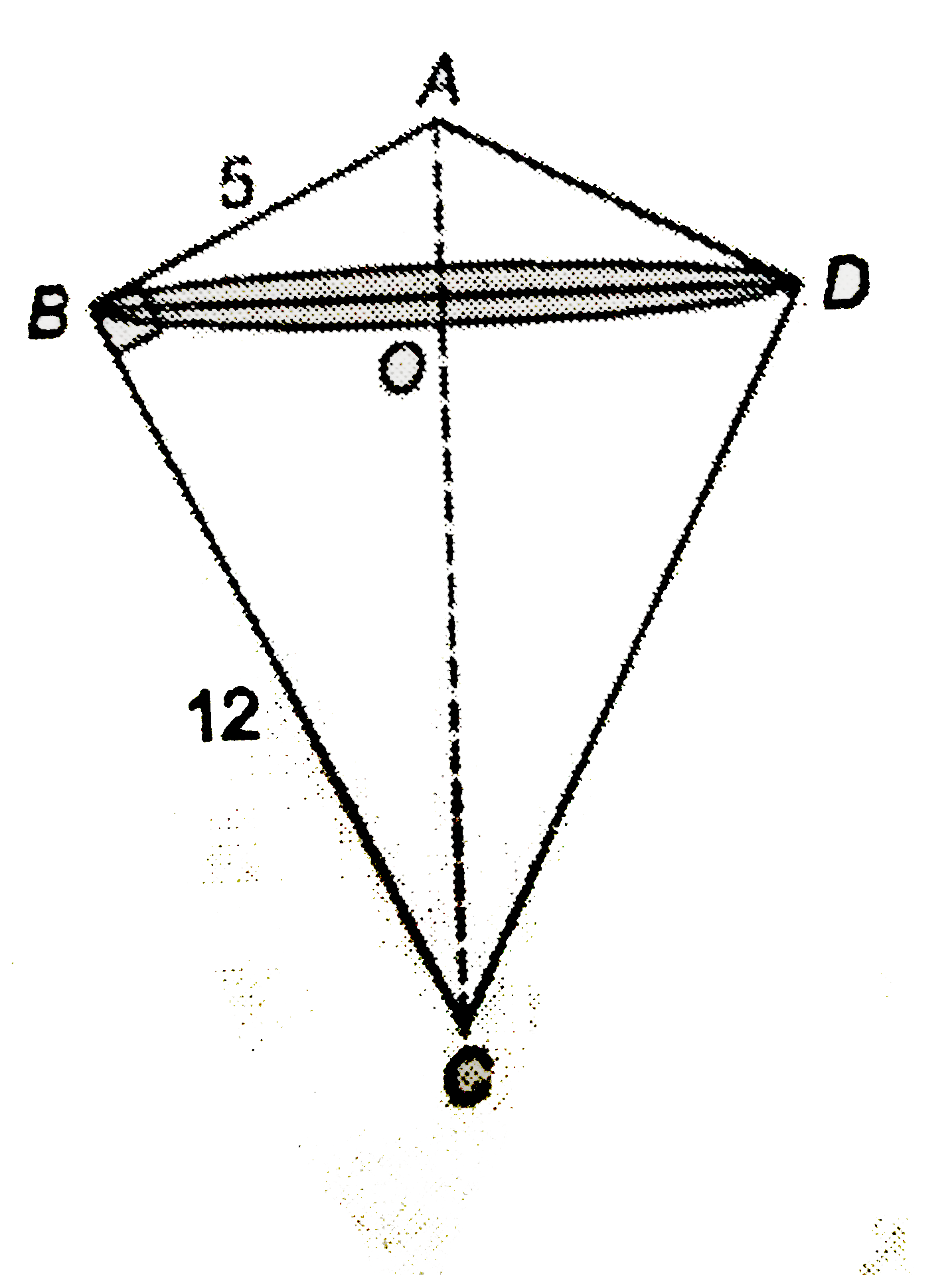
Let $Δ A B C$ is given in which
AB = 5cm
BC = 12cm
and $∠ A B C = 90^{\circ}$
Now, from Phythagoarstheorem
$A C^{2} = A B^{2} + B C^{2}$
$= 5^{2} + 12^{2}$
= 25 + 144 = 169
$\Rightarrow A C = 13 c m$
Let BO = r
Now, area of $Δ A B C = \frac{1}{2} \times A B \times B X = \frac{1}{2} \times 5 \times 12$
Again, area of $Δ A B C = \frac{1}{2} \times A C \times B O = \frac{1}{2} \times 13 \times r$
$∴ \frac{1}{2} \times 13 \times r = \frac{1}{2} \times 5 \times 12$
$\Rightarrow r = \frac{60}{13} c m$
Now, the volume of solid = volume of cone ABD + volume of cone CBD
$= \frac{1}{3} π r^{2} \times A O + \frac{1}{3} π r^{2} \times O C = \frac{1}{3} π r^{2} (A O + O C)$
$= \frac{1}{3} π r^{2} \times A C = \frac{1}{3} \times π \times \frac{60}{13} \times \frac{60}{13} \times 13 = \frac{1200 π}{13} c m^{3}$
and total surface area = curved surface of cone ABD + curved surface of cone CBD
$= π r (A B) + π r (B C)$
$= π r (A B + B C)$
$= π \times \frac{60}{13} (5 + 12)$
$= \frac{1020 π}{13} c m^{2}$

|

Class 9 MATHS SURFACE AREAS AND VOLUMES

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN-SURFACE AREA AND VOLUME-Revision Exercise (long Answer Questions)

Home
Ask Doubt
Profile