In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked products C only?
n(A)=21andn(B)=26
Number of people who like product A and B both
n(A∪B)=n(A)+n(B)−n(A∩B)
=21+26−14=33
Now n(C)=29
Number of people who like product B and C both
n(B∩C)=14
Number of people who like product C and A both
n(A∩C)=12
Number of people who like product A,B and C, all
n(A∩B∩C)=8
Then, number of people who like any one of the one product
n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)
−n(B∩C)−n(A∩C)+n(A∩B∩C)
=21+26+29−14−14−12+8
=44
∵n(A∪B∪C)=44andn(A∪B)=33
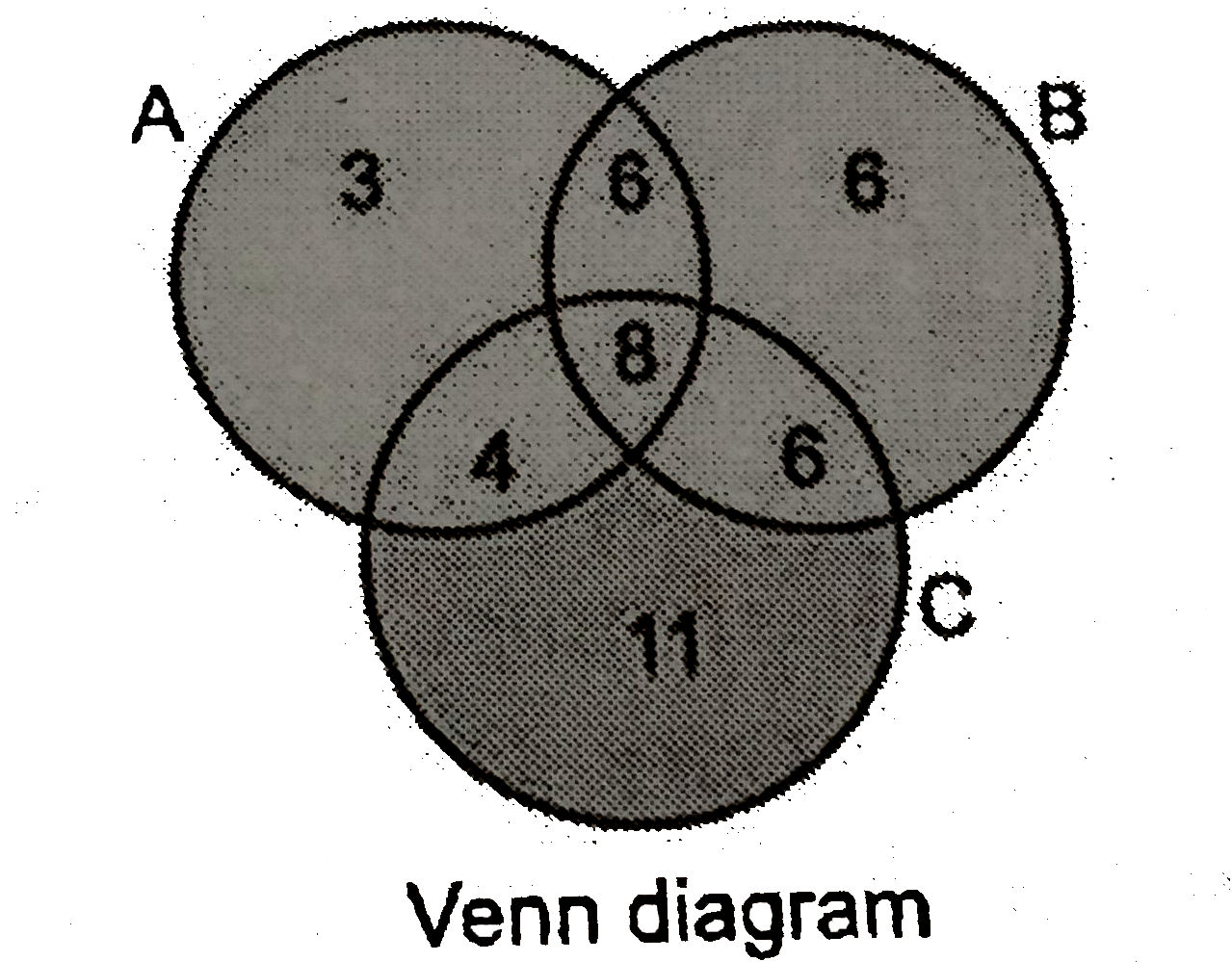
Number of people who like only product C
=n(A∪B∪C)−n(A∪B)=44−33=11
Therefore, number of people who like only product
C=11.
Topper's Solved these Questions
Similar Questions
In a survery, it was found that 21 persons liked product A, 26 liked product B and 29 liked product C. If 14 persons liked products A and B, 12 liked products C and A, 13 persons liked products B and C and 8 liked all the three products then
(i) Find the number of persons who liked the product C only
(ii) The number of persons who like the products A and B but not C
View SolutionIn a survey it is found that 21 people like product A, 26 people like product B and 29 like product C. If 14 people like products A and B, 15 people like products B and C, 12 people like products C and A, and 8 people like all the three products, find
(i) how many people are surveyed in all,
(ii) how many like product C only.
View Solution
Knowledge Check
If an amide is treated with P2O5 the likely product is an
AacidBalkyl cyanideCamineDacid anhydride.In a school, on the Republic day, three dramas A, B and C are performed on the dais. In a group of people, who attended the function and who like at least one of the three dramas, 16 people like A,20 people like B,15 people like C,4 people like both A and B,3 people like all the three. Then how many people like at most two?
A59B41C4D6
In a survey, 50 people like product A, 30 people like product B and 20 people like product C and 35 people l not like any product like exactly two products. If 5 people like all the three products then number of people who do . [There are 100 people in survey]
View SolutionOut of 10000 people surveyed, 3700 liked city A, 4000 liked city B and 5000 liked city C. 700 people liked A and B 1200 liked B and C and 1000, liked A and C. Each person liked at least one city. Then find
The number of people liking all the three cities.
View SolutionOut of 10000 people surveyed, 3700 liked city A, 4000 liked city B and 5000 liked city C. 700 people liked A and B 1200 liked A and C and 1000, liked B and C. Each person liked at least one city. Then find
The number of persons liking A and B but not C.
View Solution product +gas how many C14 atoms are present in the product
product +gas how many C14 atoms are present in the product
View SolutionOut of 10000 people surveyed, 3700 liked city A, 4000 liked city B and 5000 liked city C. 700 people liked A and B ,1200 liked A and C and 1000 liked B and C. Each person liked at least one city. Then find the number of persons liking at least two cities as a % of number of people liking exactly one city.
View Solution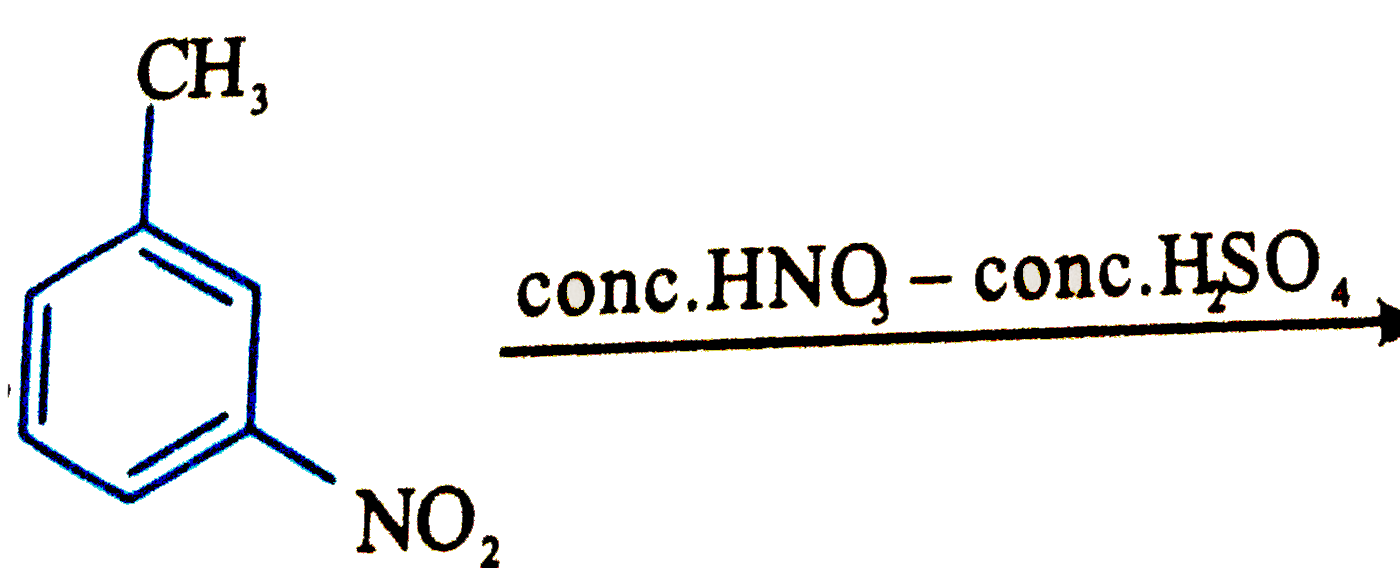
In the above reaction, product is most likely to be formed?
View Solution
