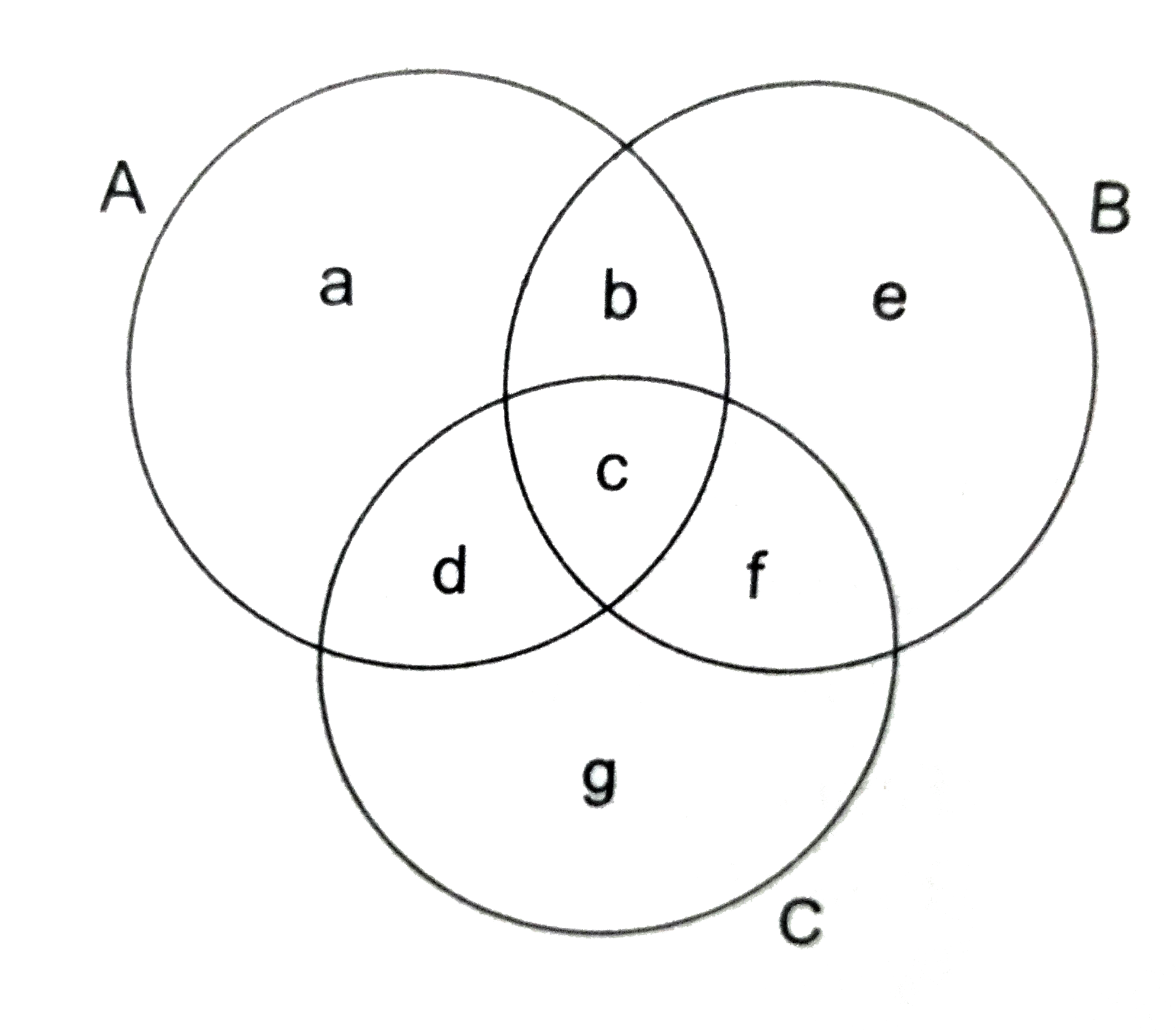
In a town of 10,000 families, it was found that 40% of the families buy newspaper A, 20% buy newspaper B, 10% buy newspaper C, 5% buy A and B, 30% buy B and C and 4% buy A and C. If 2% buy all the three newspapers, find the number of families which buy.
(i) A only,
(ii) B only,
(iii) none of A, B and C.
The correct Answer is:(i) 3300
(ii) 1400
(iii) 4000
n(A)=(40%of10000)=(40100×10000)=40000,
n(B)=(20%Of10000)=2000,n(C)=(10%of10000)=1000,
n(A∩B)=(5%of10000)=500,n(B∩C)=(3%of10000)=300,
n(A∩C)=(4%of10000)=4000,n(A∩B∩C)=(2%of10000)=200,
and n(U)=10000,
⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩a+b+c+d=4000,b+c+e+f=2000,c+d+f+g=1000, b+c=500, c+f=300, c+d=400, c=200,
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - SETSEXERCISE - EXERCISE-1H15videos
SETS
- BOOK - RS AGGARWALCHAPTER - SETSEXERCISE - EXERCISE-1F6videos
SETS
- BOOK - RS AGGARWALCHAPTER - RelationsEXERCISE - EXERCISE 2E12videos
Relations
- BOOK - RS AGGARWALCHAPTER - SOLUTION OF TRIANGLESEXERCISE - EXERCISE 18 B3videos
SOLUTION OF TRIANGLES
Similar Questions
In a town od 10,000 families , it was found that 40% families buy newspaper A, 20% buy newspaper B and 10% newspaper C, 5% buy A and B , 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers , find the number of families which buy :
(i) A only
(ii) B only
(iii) C only
(iv) none of A,B and C.View SolutionIn a town of 10,000 families it was found that 40% families buy newspaper A, 20% families buy newspaper B and 10% families buy news-paper C. 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three mewspapers, find the number of families which buy (i) A only
View Solution
Knowledge Check
- Question 1 - Select One
In a town of 10,000 families it was found that 40% families buy newspaper A, 20% families buy newspaper B and 10% families buy news-paper C. 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three mewspapers, find the number of families which buy (i) A only
A3100B3300C2900D1400 - Question 2 - Select One
In a town of 10,000 families it was found that 40% family buy newspaper A, 20% buy newspaper B and 10% families buy newspaper C, 5% families buy A and B, 3% buy Band Cand 4% buy A and C. If 2% families buy all the three newspapers, then number of families which buyA only is
A3100B3300C2900D1400 - Question 3 - Select One
In a town of 10,000 families it was found that 40% family buy newspaper A, 20% buy newspaper B and 10% families buy newspaper C, 5% families buy A and B, 3% buy Band Cand 4% buy A and C. If 2% families buy all the three newspapers, then number of families which buyA only is
A3100B3300C2900D1400
In a town of 10,000 families it was found that 40% families buy newspaper A, 20% families buy newspaper B and 10% families buy news-paper C. 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three mewspapers, find the number of families which buy (ii) B only
View SolutionIn a town of 10,000 families it was found that 40% family buy newspaper A, 20% buy newspaper B and 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2%families buy all the three newspapers, then find the number of families which buy A only
View SolutionIn a town of 10,000 families it was found that 40% families buy newspaper A, 20% families buy newspaper B and 10% families buy news-paper C. 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three mewspapers, find the number of families which buy (iii) none of A, B and C
View SolutionIn a town of 10000 families, it was found that 40% families buy newspaper A, 20% families buy newspaper B, 10 % families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4 % buy a and C. If 2% families buy all the three newspaper. Find
(i) the number of familiar which buy newspaper A only.
(ii) the number of familiar which buy none of A , B and C.View SolutionIn a town of 10000 families it was found that 40% family buy newspaper A, 20% family buy newspaper B and 10% family buy newspaper C. 5% families buy A and B, 3% families buy A and C. If 2% families buy all the three newspapers. Then, number of families which buy A only is
View Solution

