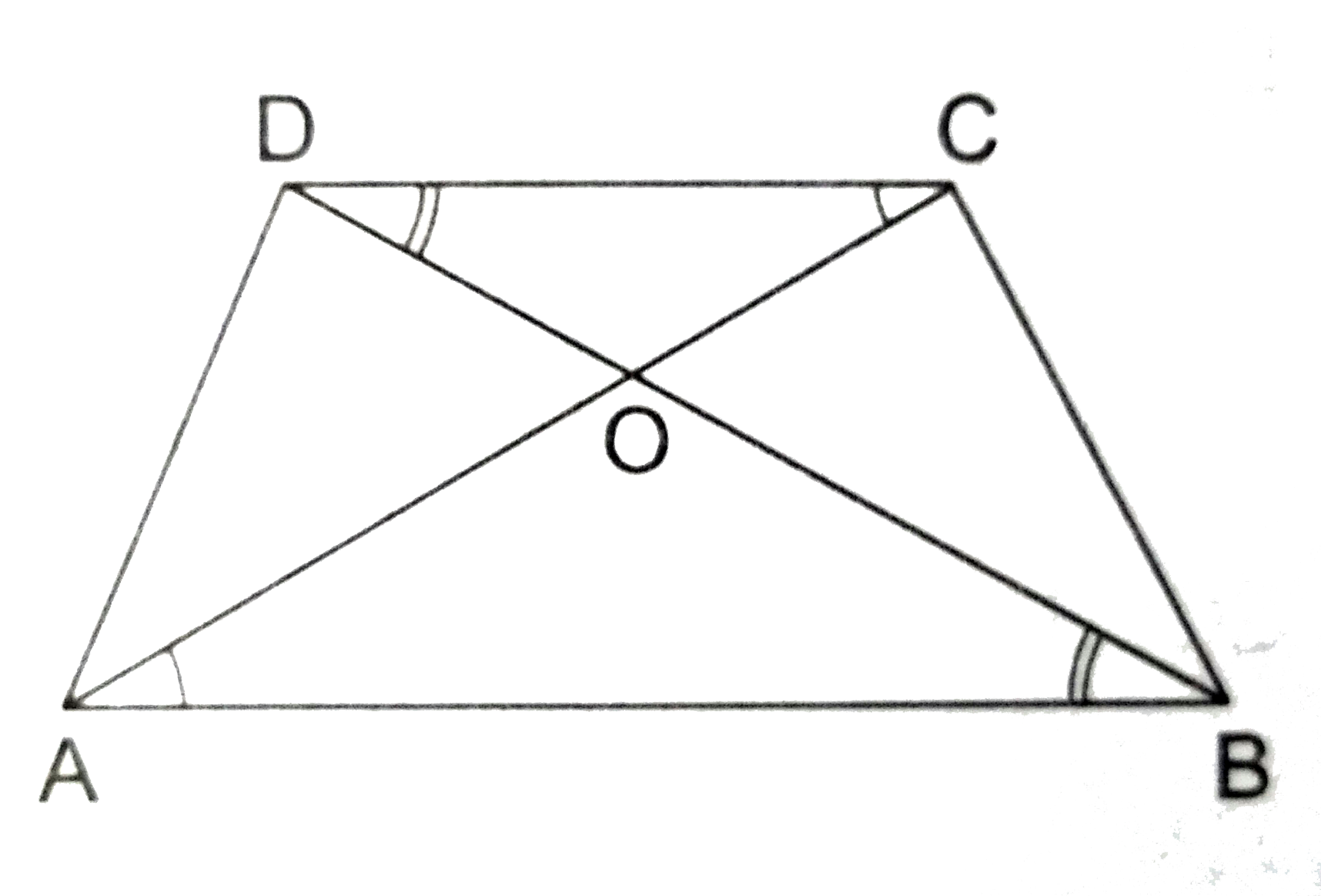
In a trapezium $A B C D$ , $O$ is the point of intesection of $A C$ and $B D$ , $A B ∣ ∣ C D$ and $A B = 2 \times C D$ . If the area of $△ A O B = 84 c m^{2}$ . Find the area of $△ C O D$ .

A

$21 c m^{2}$

B

$22 c m^{2}$

C

$23 c m^{2}$

D

$24 c m^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

In $Δ A O B and Δ C O D$ , we have
$∠ O A B = ∠ O C D$ [ alt. int. $∠$ ]
and $∠ O B A = ∠ O C D$ [ alt. int. $∠$ ]
$∴ Δ A O B ~ Δ C O D$ [ by AA- similarity]
$\Rightarrow \frac{a r (Δ A B C)}{a r (Δ C O D)} = \frac{A B^{2}}{C D^{2}} = \frac{{(2 C D)}^{2}}{C D^{2}} [∴ A B = 2 \times C D]$
$= \frac{4 \times C D^{2}}{C D^{2}} = 4$
$\Rightarrow a r (Δ C O D) = \frac{1}{4} \times a r (Δ A O B) = (\frac{1}{4} \times 84) c m^{2} = 21 c m^{2}$
Hence, the are of the $Δ C O D$ is $21 c m^{2}$

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In trapezium ABCD, AB || CD and AB = 2 CD. Its diagonals intersect at O. If the area of $Δ A O B = 84 c m^{2}$ , then the area of $Δ C O D$ is equal to
A $72 c m^{2}$
B $21 c m^{2}$
C $42 c m^{2}$
D $26 c m^{2}$
Question 2 - Select One
ABCD is a square , E is a point on AB such that BE=17 cm. The area of triangle ADE is 84 $c m^{2}$ . What is the area of square ?

A $400 c m^{2}$
B $625 c m^{2}$
C $729 c m^{2}$
D $576 c m^{2}$
Question 3 - Select One
$A B C D$ is a trapezium, such that $A B = C D$ and $A D ∣ ∣ B C . A D = 10 c m and B C = 18 c m$ . If the area of $A B C D$ is $70 c m^{2},$ what is the value (in cm) of CD?
A5
B $\sqrt{29}$
C $\sqrt{41}$
D6

RS AGGARWAL-TRIANGLES-Test Yourself

Home
Ask Doubt
Profile