In a triangle ABC, side AB has equation 2x+3y=29 and side AC has equation x+2y=16. If the midpoint of BC is (5, 6), then find the equation of BC.Solution in Bengali
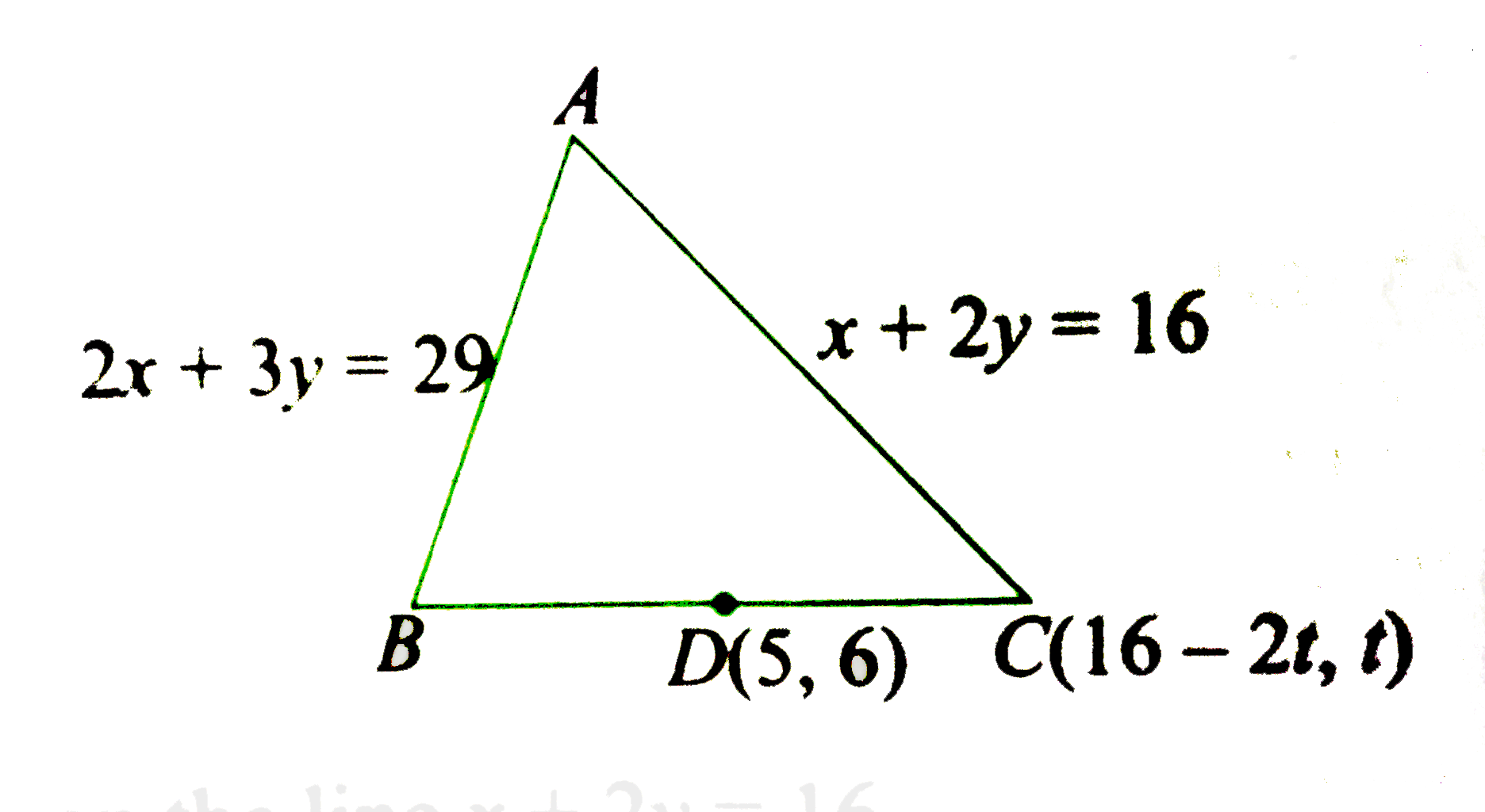
Vertex C lies on the line x+2y = 16.
So, let point C be (16-2t,t).
D(5,6) is midpoint of BC.
So, point B is (2t-6, 12-t)
Point B lies on the line 2x+3y-29 = 0
∴2(2t−6)+3(12−t)−29=0
⇒t=5
Hence, point B is (4,7)
Therefore, equation of line BC is
y−7=6−75−4(x−4)
or x+y = 11
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXAMPLE
12 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.1
23 Videos
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
Show that the lines 4x+y−9=0,x−2y+3=0,5x−y−6=0 make equal intercepts on any line of slope 2.
View SolutionFind the equation of the right bisector of the line segment joining the points (3,4) and (-1,2).
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionIn a triangle ABC, side AB has equation 2x+3y=29 and side AC has equation x+2y=16. If the midpoint of BC is 5, 6), then find the equation of BC.
View SolutionIf the middle points of the sides BC,CA, and AB of triangle ABC are (1,3),(5,7), and (−5,7), respectively, then find the equation of the side AB.
View SolutionIn triangle ABC , the equation of the right bisectors of the sides AB and AC are x+y=0 and y−x=0 , respectively. If A≡(5,7) , then find the equation of side BC.
View SolutionIn a triangle ABC, side AB has equation 2x+3y=29 and side AC has equation x+2y=16. If the midpoint of BC is (5, 6), then find the equation of BC
View SolutionThe equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View SolutionIn a triangle ABC, side AB has equation 2x+3y=29 and side AC has equation x+2y=16. If the midpoint of BC is 5, 6), then find the equation of BC.
View SolutionIf the middle points of the sides BC,CA, and AB of triangle ABC are (1,3),(5,7), and (−5,7), respectively, then find the equation of the side AB.
View SolutionThe sides ABandAC of a triangle ABC are respectively 2x+3y=29andx+2y=16 respectively. If the mid-point of BCis(5,6) then find the equation of BC.
View SolutionThe equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View Solutionएक त्रिभुज ABC में भुजा AB का समीकरण 2 x + 3y = 29 है तथा भुजा AC का समीकरण x + 2y = 16 है। यदि भुजा BC का मध्य बिन्दु (5, 6) है, तो BC का समीकरण है
View SolutionIn a triangle ABC, side AB has equation 2x+3y=29 and side AC has equation x+2y=16. If the midpoint of BC is (5, 6), then find the equation of BC.
View Solution
