In a triangle ABC, ∠A=302,BC=2+√5, then find the distance of the vertex A from the orthocenter
Video Solution
Text Solution
The correct Answer is:(2+√5)√3
Distance of vertex a from orthocenter H given by is
AH=2RcosA
we have,
R=a2sinA=2+√52sin30∘=2+√52×12=(2+√5)
∴AH=2(2+√5)cos302
=(2+√5)√3
|
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.10
Explore 8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.11
Explore 4 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.8
Explore 7 Videos
- PROGRESSION AND SERIESBook:CENGAGEChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBook:CENGAGEChapter:PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEExercise:Question Bank
Explore 32 Videos
Similar Questions
Knowledge Check
In a triangle ABC, BC = √39, AC = 5 and AB = 7. What is the measure of the angle A?
Aπ4Bπ3Cπ2Dπ6In a triangle ABC,vertex angles A,B,C and side BC are given .The area of ΔABC is
As(s−a)(s−b)(s−c)2Bb2sinCsinAsinBCab sin CD12a2sinBsinCsinAIn ΔABCanl≥A=π6&b:c=2:√3then ∠B is
Aπ3Bπ2Cπ4DNon of these
Distance of the orthocenter H from vertex B is
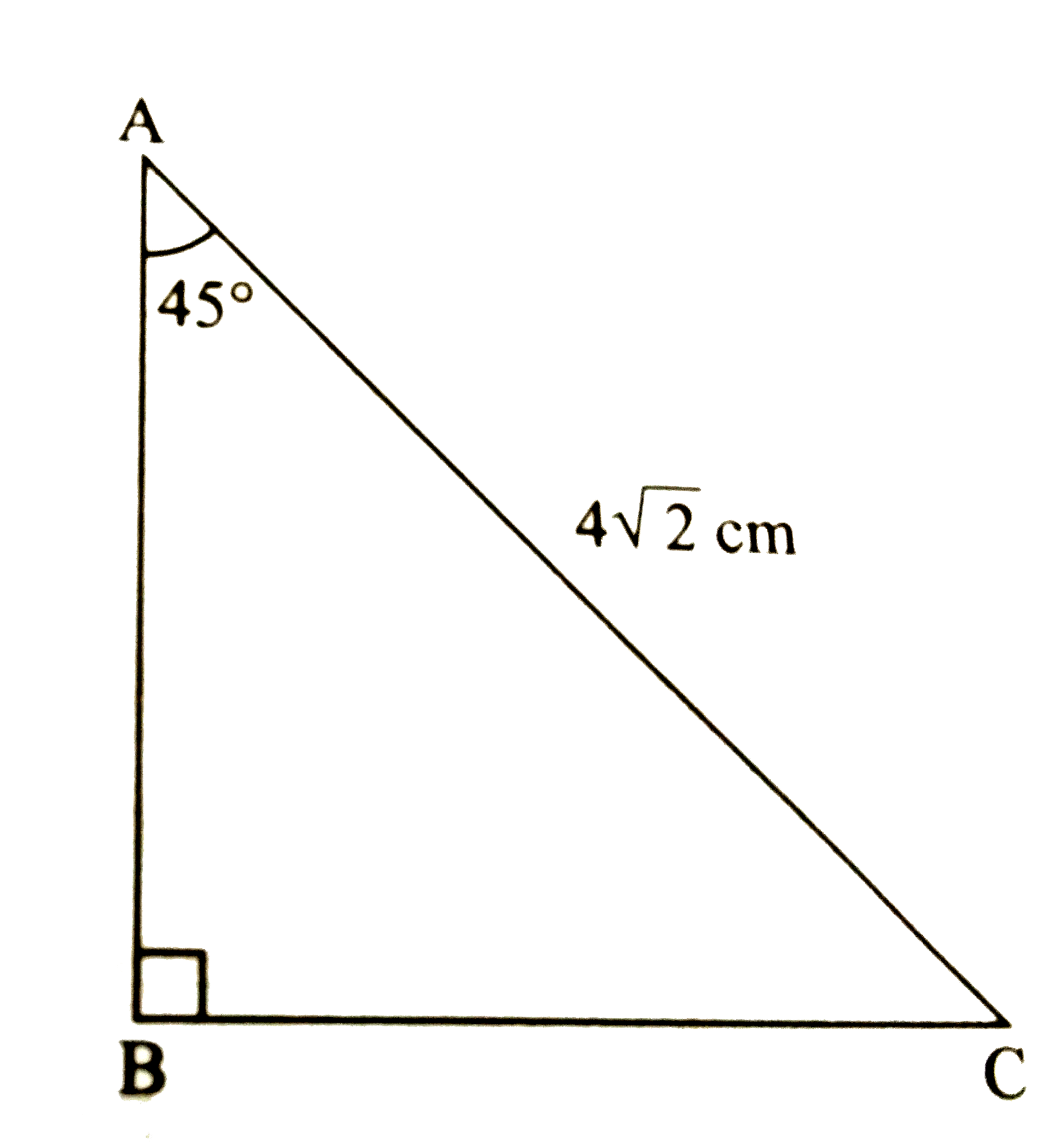
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
View SolutionIn a ΔABC,∠B=90∘andAC=8√2. If AB=BC, then find AB.
View SolutionIn a triangle ABC, AB=BC and ∠A=60∘. Find ∠B.
View SolutionIn a triangle ABC if ∠ABC=60∘, then (AB−BC+CAr)2=
View Solution
