In a triangle ABC, it is known that AB=AC. Suppose D is the mid-point of AC and BD=BC=2. Then the area of the triangle ABC is-
2
2√2
√7
2√7
The correct Answer is:C

We know
AB2+BC2=2(CD2+BD2)
AB2+4=2(AB24+4)
AB2+4=AB24+8
AB22=4
AB2=8
AB=2√2
Now
Area =12×2×√7=√7
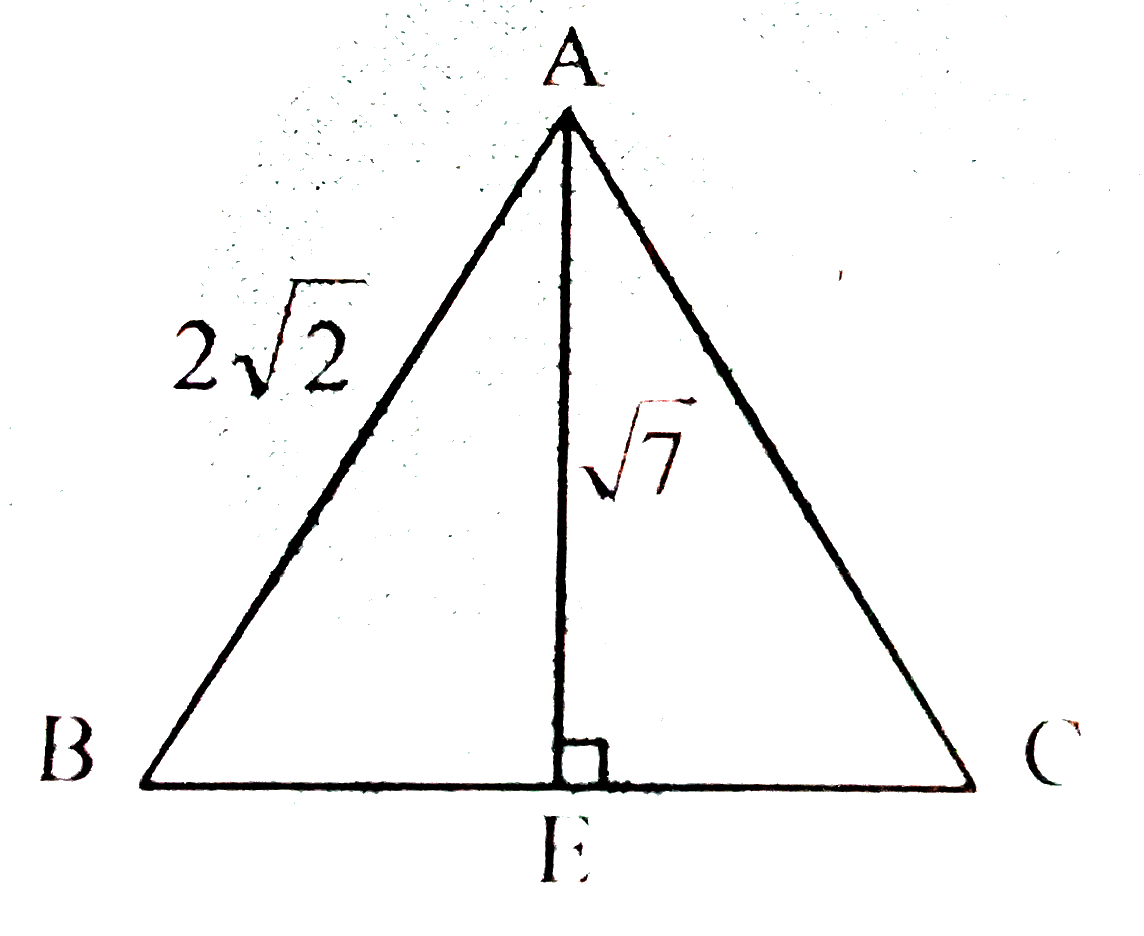
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2(MATHEMATICS)
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART -I MATHEMATICS
20 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-I MATHEMATICS
15 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Knowledge Check
In ΔABC,∠B is a right angle, AC=6 cm, D is the mid point of AC. The length of BD is
 A4 cmB√6 cmC3 cmD3.5 cm
A4 cmB√6 cmC3 cmD3.5 cmIn a ΔABC, D is the mid point of side AC such that BD =12 AC .∠ABC is ?.
A45∘B30∘C90∘DNone of theseIn a triangle ABC, the angle bisector BD of ∠B intersects AC in D. Suppose BC=2,CD=1andBD=3√2. The perimeter of the triangle ABC is
A172B152C174D154
In a triangle ABC, the angle bisector BD of ∠B intersects AC in D. Suppose BC=2,CD=1andBD=3√2. The perimeter of the triangle ABC is
View SolutionIn a triangle ABC,∠B=90∘,D is the midpoint of AC,BD=√117. Sum of sides of AB & BC is 30 cm. Find the area of triangle ABC.
View SolutionGiven a triangle ABC with AB=2 and AC=1. Internal bisector of ∠BAC intersects BC at D. If AD = BD and Δ is the area of triangle ABC, then find the value of 12Δ2.
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
View SolutionABC is a triangle and D is the mid-point of BC . The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
View Solution
