In a triangle, locate a point in its interior which is equidistant from all the sides of the triangle.
To locate a point in the interior of a triangle that is equidistant from all three sides, we can follow these steps:
1. Draw Triangle ABC: Start by sketching triangle ABC with vertices A, B, and C.
2. Construct Angle Bisectors:
- Draw the angle bisector of angle B. This is the line that divides angle B into two equal angles.
- Next, draw the angle bisector of angle C. This line divides angle C into two equal angles.
3. Identify Intersection Point:
- Let the angle bisector of angle B intersect the opposite side AC at point P.
- Let the angle bisector of angle C intersect the opposite side AB at point Q.
- The two angle bisectors (from B and C) will intersect at a point, which we will call point R.
4. Verify Equidistance:
- By the Angle Bisector Theorem, point R is equidistant from the sides AB and BC. This means the perpendicular distance from point R to side AB is equal to the perpendicular distance from point R to side BC.
- Similarly, if you were to draw the angle bisector from angle A, it would also intersect at point R, confirming that R is equidistant from side AC as well.
5. Conclusion:
- Therefore, point R, where all three angle bisectors intersect, is the point that is equidistant from all three sides of triangle ABC. This point is known as the incenter of the triangle.
- Draw the angle bisector of angle B. This is the line that divides angle B into two equal angles.
- Next, draw the angle bisector of angle C. This line divides angle C into two equal angles.
- Let the angle bisector of angle B intersect the opposite side AC at point P.
- Let the angle bisector of angle C intersect the opposite side AB at point Q.
- The two angle bisectors (from B and C) will intersect at a point, which we will call point R.
- By the Angle Bisector Theorem, point R is equidistant from the sides AB and BC. This means the perpendicular distance from point R to side AB is equal to the perpendicular distance from point R to side BC.
- Similarly, if you were to draw the angle bisector from angle A, it would also intersect at point R, confirming that R is equidistant from side AC as well.
- Therefore, point R, where all three angle bisectors intersect, is the point that is equidistant from all three sides of triangle ABC. This point is known as the incenter of the triangle.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-1 )35videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-2 )10videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.4)6videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner20videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
What is the number of points in the plane of a triangle ABC which are at equal distance from the vertices of the triangle ?
A0B1C2D3 - Question 2 - Select One
The point in the plane of a triangle which is at equal perpendicular distance from the sides of the triangle is :
AcentroidBincentreCcircumcentreDorthocentre - Question 3 - Select One
The coordinates of the point which is equidistant from the three vertices of the △AOB as shown in the figure is
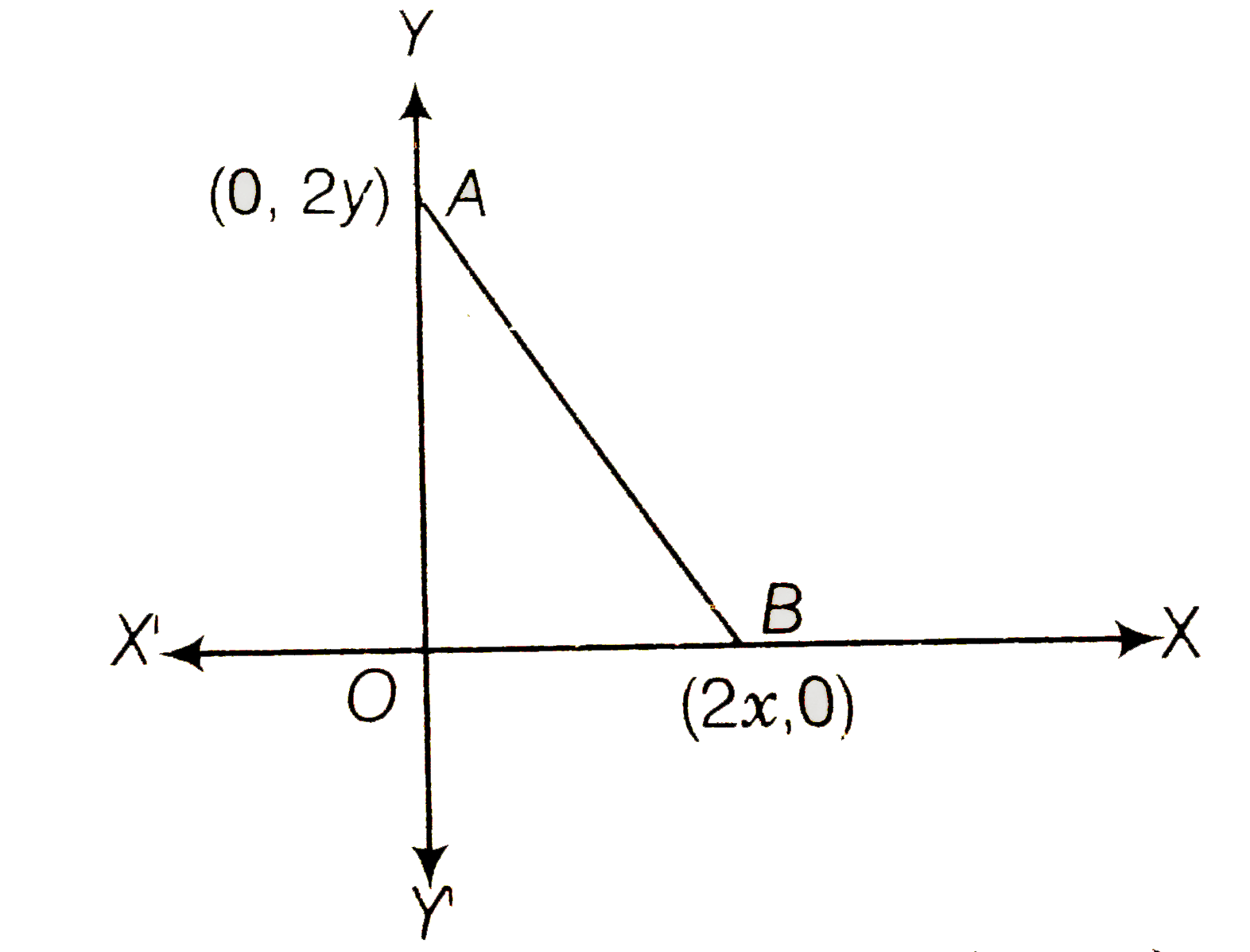 A(x,y)B(y,x)C(x2,y2)D(y2,x2)
A(x,y)B(y,x)C(x2,y2)D(y2,x2)
Find the locus of the point which is equidistant from the sides AB and AC of triangle ABC.
View SolutionThree charges of 1 nC, 2 nC and 3 nC are placed at the corners of an equilateral triangle of side √3m. Calculate electrostatic potential at a point equidistant from the three corners of the triangle.
View SolutionIncentre of a triangle lies in the interior of :
View SolutionIncentre of a triangle lies in the interior of :
View SolutionThe loucs of the point which is equidistant from the three determined by the sides of a triangles is _______
View Solution
