In AD⊥BC, prove that AB2+CD2=BD2+AC2Solution in Tamil
Let point B and C lie on the x-axis such that BD=DC, where, D(0,0) is midpoint of BC.
Let point A be (x,y).
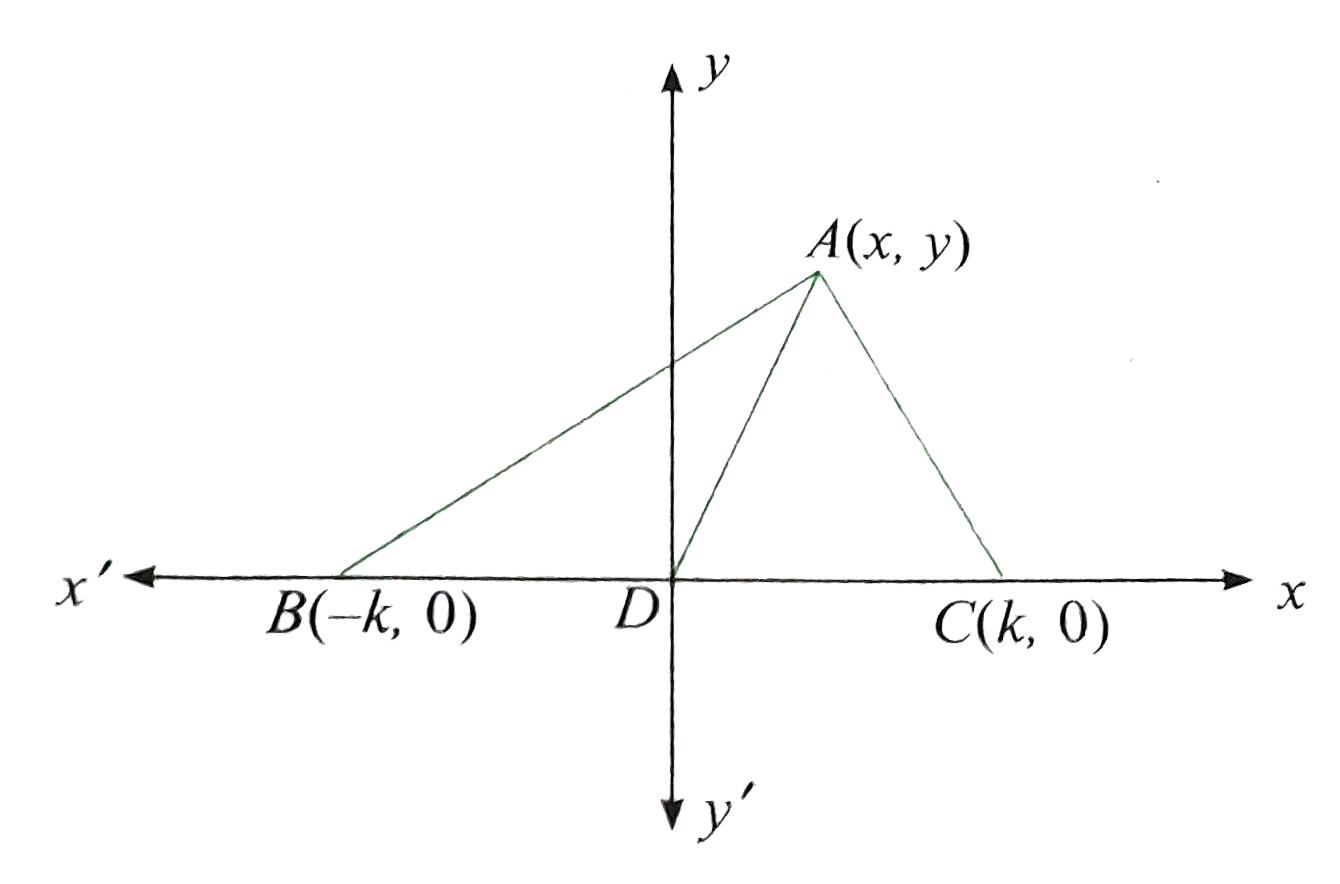
BD=k.So, point B is (−k,0) and point C is (k,0).
Now, AB2+AC2=(x+k)2+(y−0)2+(x−k)2+(y−0)2
=x2+k2+2xk+y2+x2k2−2xk+y2
=2x2+2y2+2k2=2(x2+y2+k2)
And 2(AD2+BD2)=2[(x−0)2+(y−0)2+k2]
=2(x2+y2+k2)
Therefore, AB2+AC2=2(AD2+BD2)
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.2
8 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
What is the minimum area of a triangle with integral vertices ?
View SolutionThe distance between the points (acosα,asinα) and (acosβ,asinβ) is
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View Solutionआकृति 6.48 में ∠ACB=90∘ तथा CD⊥AB है। सिद्ध कीजिए की BC2AC2=BDAD है
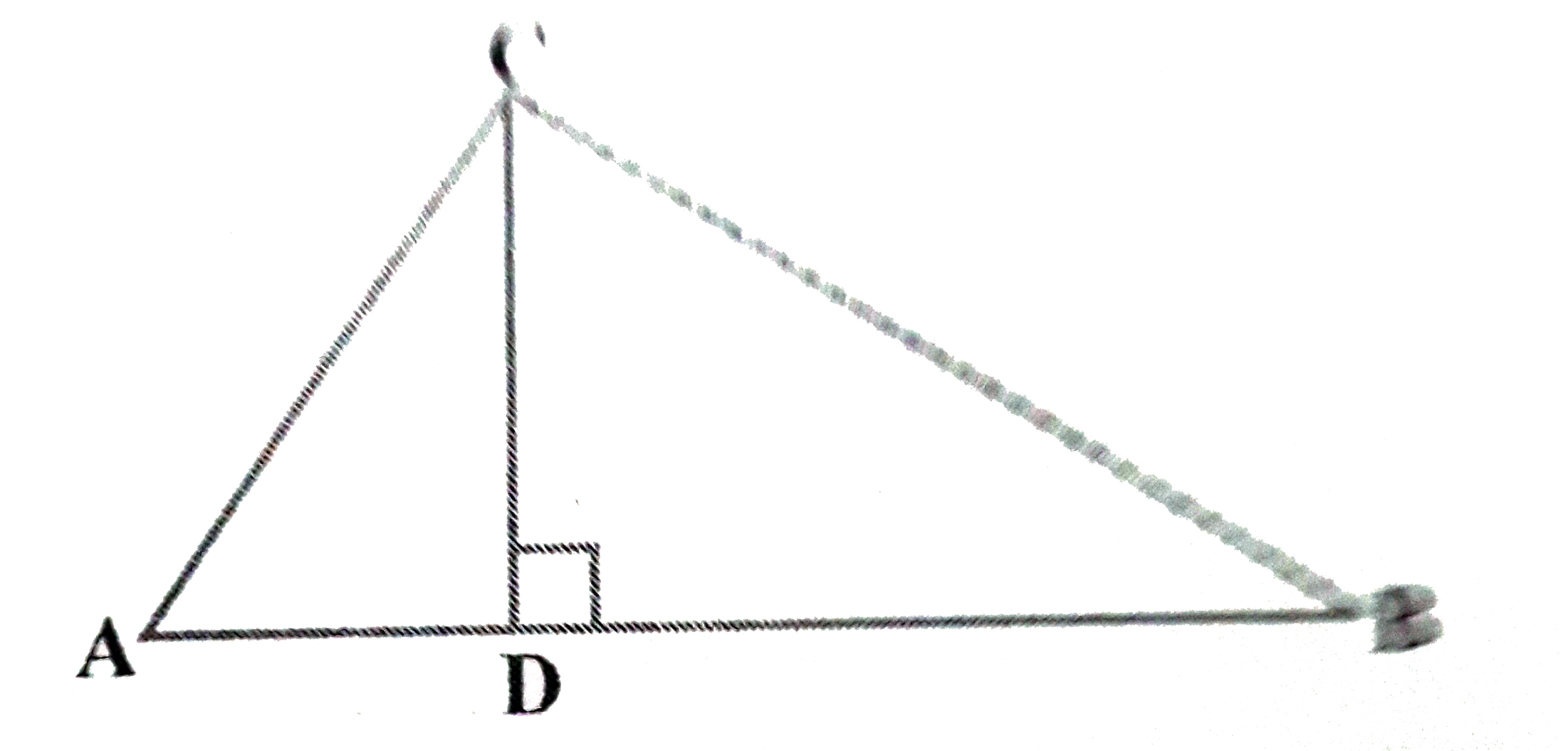
View Solutionआकृति 6 .50 में AD⊥BC है सिद्ध कीजिए कि AB2+CD2=BD2+AC2 है

View SolutionIn the given figure ∠ABC=90∘andCD⊥AB. Prove that BC2AC2=BDAD
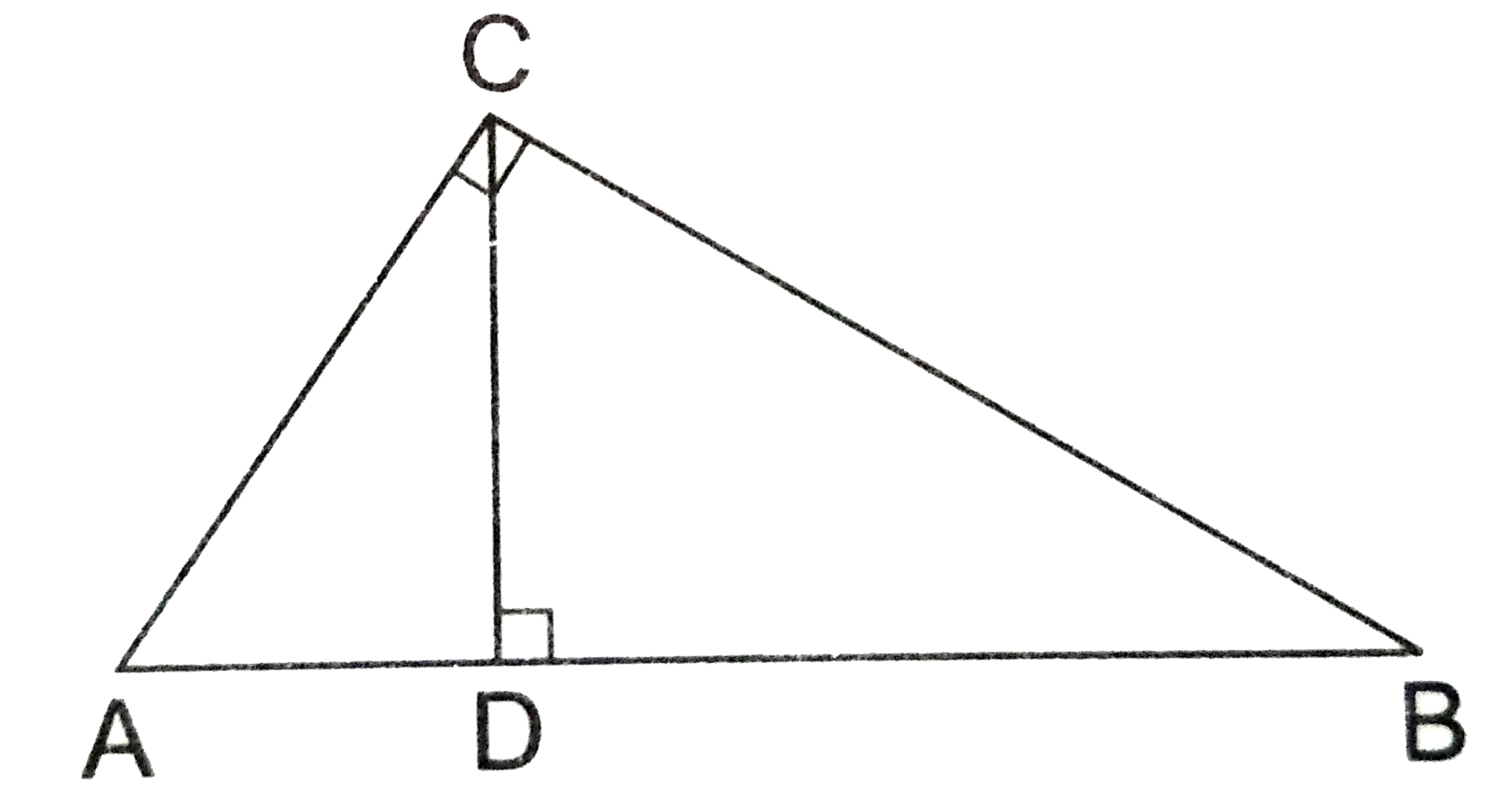
View SolutionIn AD⊥BC, prove that AB2+CD2=BD2+AC2
View SolutionIn Δ ABC , AD ⊥BC and AD2=BD×CD. Prove that AB2+AC2= (BD+CD)2

View SolutionIn the given figure , BD ⊥ AC .Prove that AB2+CD2=AD2+BC2
View Solution△ABC ಯಲ್ಲಿ AD⊥BC ಮತ್ತು AD2=BDxCD ಆಗಿದೆ. ಹಾಗಾದರೆ AB2+AC2=(BD+CD)2 ಎಂದು ಸಾಧಿಸಿ.
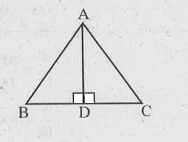
View SolutionIn ΔACB,∠C=90∘ and CD⊥ AB
Prove that BC2AC2=BDAD.
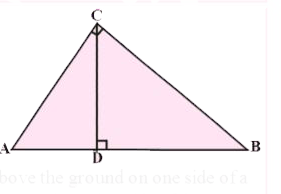
View SolutionIn the given fig. if AD ⊥BC
Prove that AB2+CD2=BD2+AC2 .
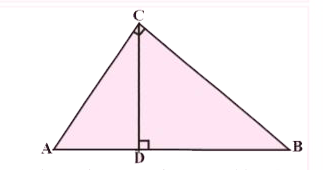
View SolutionIn the given fig. if AD ⊥BC
Prove that AB2+CD2=BD2+AC2 .
View SolutionIn ΔACB,∠C=90∘ and CD⊥ AB
Prove that BC2AC2=BDAD.
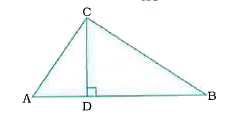
View SolutionIn the given figure, ∠ACB=90∘ and CD⊥AB. Prove that BC2AC2=BDAD.
View Solution
