In addition to the standard airfare, a particular airline charges passengers for two kinds of travel service: $25 to check a bag and $15 to upgrade to priority boarding. If the airline collected $3,065 in baggege and priority boarding fees from 145 travel services on two flights combined, which of the following system of equations could be used to determine the number of bags checked (b) and the number of priority boarding upgrades (p) purchased on the two flights?
b+p=145×2
25b+15p=3,065×2
b+p=145
25b+15p=3,065
b+p=145
15b+25p=3,065
b+p=1452
15b+25p=3,0652
The correct Answer is:B
To solve the problem, we need to set up a system of equations based on the information provided.
Step 1: Define the Variables
Let:
- b = number of bags checked
- p = number of priority boarding upgrades purchased
Step 2: Set Up the First Equation
According to the problem, the airline collected a total of $3,065 from baggage and priority boarding fees. The fee for checking a bag is $25, and the fee for upgrading to priority boarding is $15. Therefore, the total amount collected can be expressed as:
25b+15p=3065
Step 3: Set Up the Second Equation
The problem also states that there were a total of 145 travel services (which includes both bags checked and priority boarding upgrades). This can be expressed as:
b+p=145
Step 4: Write the System of Equations
Now we can write the system of equations based on the two equations we have set up:
1. 25b+15p=3065
2. b+p=145
Final System of Equations
Thus, the system of equations that can be used to determine the number of bags checked (b) and the number of priority boarding upgrades (p) is:
25b+15p=3065b+p=145
Let:
- b = number of bags checked
- p = number of priority boarding upgrades purchased
According to the problem, the airline collected a total of $3,065 from baggage and priority boarding fees. The fee for checking a bag is $25, and the fee for upgrading to priority boarding is $15. Therefore, the total amount collected can be expressed as:
25b+15p=3065
The problem also states that there were a total of 145 travel services (which includes both bags checked and priority boarding upgrades). This can be expressed as:
b+p=145
Now we can write the system of equations based on the two equations we have set up:
1. 25b+15p=3065
2. b+p=145
Thus, the system of equations that can be used to determine the number of bags checked (b) and the number of priority boarding upgrades (p) is:
25b+15p=3065b+p=145
Topper's Solved these Questions
Similar Questions
The lateral area of the right circular cone is 60π. If the radius of the base is 6, what is the volume of the cone
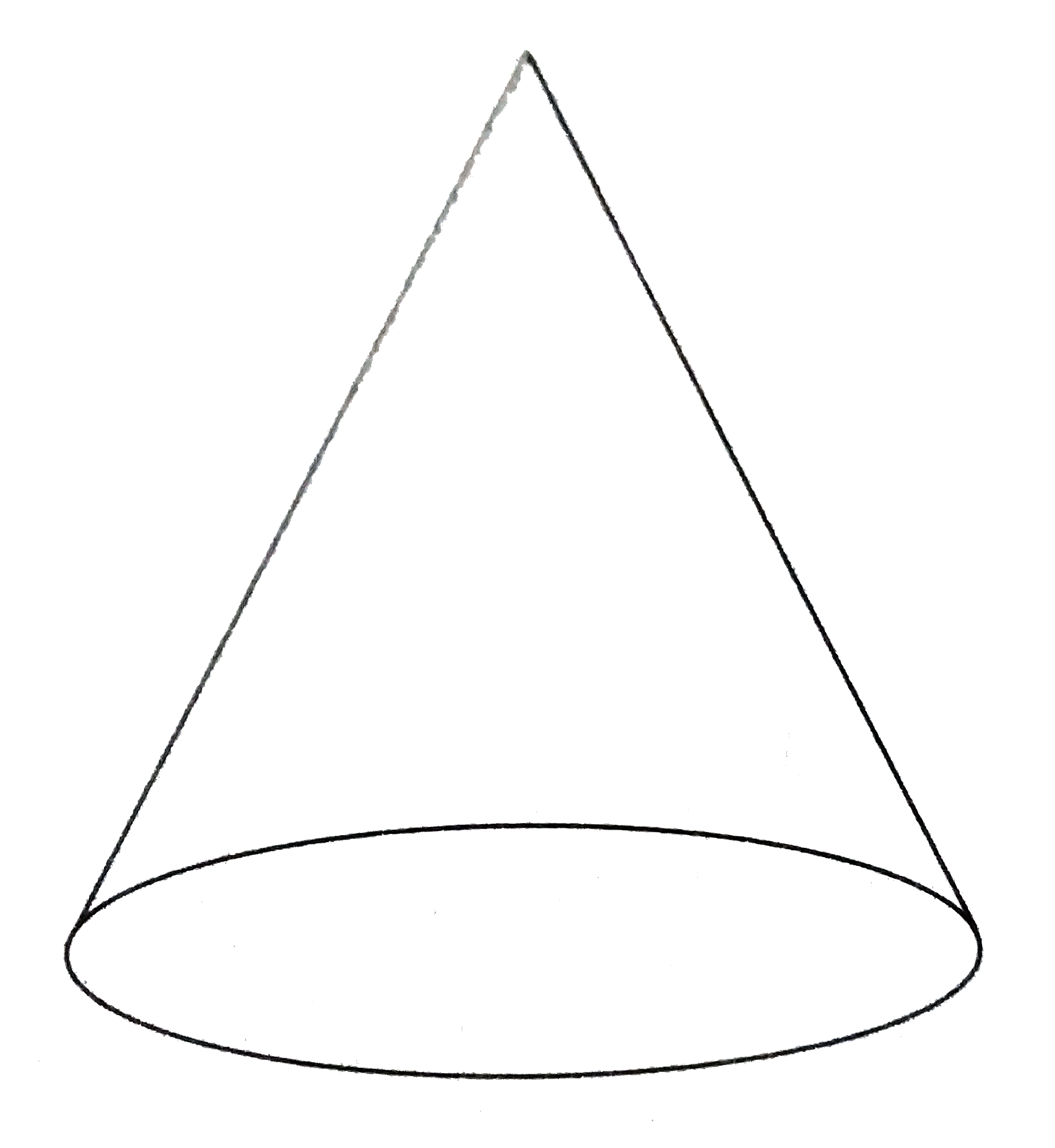
View SolutionIf x≠±1, then x+1x−1−x−1x+1=
View SolutionStatement : The airlines have requested all their bona fide passengers to check the status of flight operations before leaving their homes as heavy fog is causing immense problems to normal flight operations.
Which of the following assumption(s) is/are implicit in the above statement ?
(A) The majority of the air passengers may check the flight status before starting their journey to the airport.
(B) The Government may take serious objection to the notice issued by the airline company.
(C) Majority of the passengers may cancel their tickets and postpone their journey till the situation becomes normal.
View Solution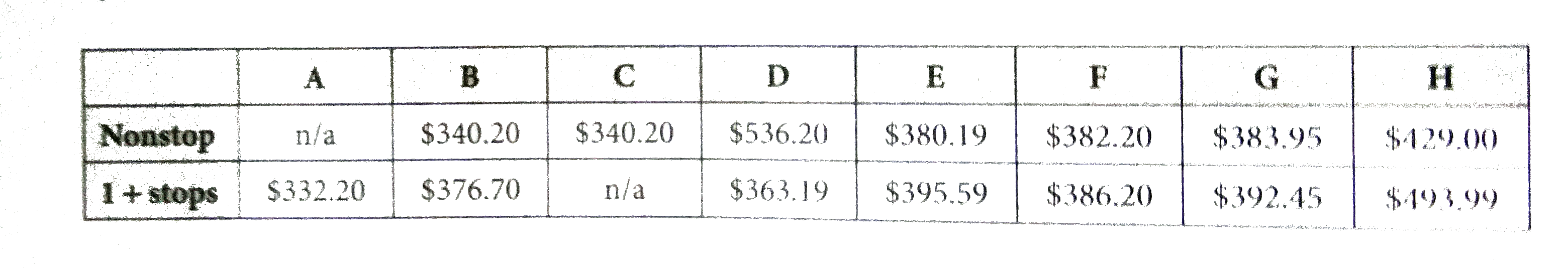
Airlines C and F offer six nonstop flights each to San Francisco throughout the day at the prices shown in the table. Each flights on each airline can hold 170 passengers. If all six of Airlines C's flights are filled to capacity and all six of Airline E's flights are filled to 90% capacity on a paritcular day, how many more revenue does Airline E generate than Airline C on that day?
View SolutionIf the airlines fail to inform their passengers of the _________, then such passengers will be entitled for a __________ in addition to the ticket refund.
View SolutionThe ratio of 1st and 2nd classes train fairs between two stations is 3 : 1 and that of the number of pas- sengers travelling between these stations by 1st and 2nd classes is 1 : 50. If on a particular day, X 2650 be collected from the passengers travelling between these stations, then find the amount collected from 2nd class passengers.
View SolutionWhich of the following airlines is the nationalized airline of India?
View SolutionHow many total squares are there in a standard chess board (or check board)?
View SolutionHow many total rectangles are there in a standard chess board (or check board)?
View SolutionThe ratio of the first and second class train fares be tween two stations is 3 : 1 and that of the numbers of passengers travelling between the two stations by first and second classes is 1:50. If on a particular day, Rs 1,325 is collected from passengers travelling between the two stations then the amount collected from the second class passengers is :
View SolutionEffect: Govt has allowed all the airlines to charges additional among as peak time congestion charges for the flights landing between 6.00 a.m. and 10.00 a.m. Which of the following is a probable cause of the above effect? 1)All the airline companies had threatened to suspend their services during peak hours. The Govt. has increased its tax for peak time flights. 3) The aircrafts are routinely put on hold over the airports while landing during peak time, causing extra fuel consumption. 4) The airline companies can now charge unlimited additional charges for peak time flights. 5) None of these
View SolutionStatement:An advertisement by Easy Air a private airlines "Travel to meerut by our airlines and get a chance to win an all expenses paid holiday to Bangkok's
Assumptions:I.Easy air flights are available for Bangkok
II.The city of meerut has an airport.
Choose the correct answer.
View SolutionThe ratio of the first and second class train fares be tween two stations is 3 : 1 and that of the numbers of passengers travelling between the two stations by first and second classes is 1:50. If on a particular day, Rs 1,325 is collected from passengers travelling between the two stations then the amount collected from the second class passengers is :
View SolutionThe ratio of the rail fares of first class and second class between the stations is 3:1 .The ratio of first class passenger and second class passengers is 1:50 .One day Rs. 1,325 is received as rail fare from passengers travelling both sides then the fare received from second class passangers is ?
View SolutionStatement : The airlines have requested all their bona fide passengers to check the status of flight operations before leaving their homes as heavy fog is causing immense problems to normal flight operations.
Which of the following assumption(s) is/are implicit in the above statement ?
(I) The majority of the air passengers may check the flight status before starting their journey to the airport.
(II) The Govt may take serious objection to the notice issued by the airline company.
(III) Majority of the passengers may cancel their tickets and postpone their journey till the situation becomes normal.
View Solution
