In an A.P., the sum of terms equidistant from the beginning and end is equal to
first term
second term
sum of first and last term
last term
The correct Answer is:C
To solve the problem, we need to understand the properties of an Arithmetic Progression (A.P.) and how the terms relate to each other.
1. Understanding the A.P.:
An A.P. is defined by its first term a and a common difference d. The n-th term of an A.P. can be expressed as:
an=a+(n−1)d
2. Identifying Terms Equidistant from Beginning and End:
If we have n terms in the A.P., the terms that are equidistant from the beginning and the end can be represented as:
- The k-th term from the start: ak=a+(k−1)d
- The k-th term from the end: an−k+1=a+(n−k)d
3. Sum of Equidistant Terms:
The sum of these two terms is:
ak+an−k+1=(a+(k−1)d)+(a+(n−k)d)
Simplifying this, we get:
=2a+(k−1)d+(n−k)d=2a+(n−1)d
4. Conclusion:
Thus, the sum of terms equidistant from the beginning and the end of an A.P. is constant and equal to:
2a+(n−1)d
This expression represents the sum of the first and last term of the A.P.
An A.P. is defined by its first term a and a common difference d. The n-th term of an A.P. can be expressed as:
an=a+(n−1)d
If we have n terms in the A.P., the terms that are equidistant from the beginning and the end can be represented as:
- The k-th term from the start: ak=a+(k−1)d
- The k-th term from the end: an−k+1=a+(n−k)d
The sum of these two terms is:
ak+an−k+1=(a+(k−1)d)+(a+(n−k)d)
Simplifying this, we get:
=2a+(k−1)d+(n−k)d=2a+(n−1)d
Thus, the sum of terms equidistant from the beginning and the end of an A.P. is constant and equal to:
2a+(n−1)d
This expression represents the sum of the first and last term of the A.P.
Topper's Solved these Questions
- PROGRESSIONS BOOK - ML KHANNACHAPTER - PROGRESSIONS EXERCISE - PROBLEM SET - 1 (TRUE AND FALSE)
10 Videos
- PROGRESSIONS BOOK - ML KHANNACHAPTER - PROGRESSIONS EXERCISE - PROBLEM SET - 1 (FILL IN THE BLANKS)
4 Videos
- PROBABILITYBOOK - ML KHANNACHAPTER - PROBABILITYEXERCISE - MISCELLANEOUS EXERCISE
6 Videos
- PROPERTIES OF TRIANGLES BOOK - ML KHANNACHAPTER - PROPERTIES OF TRIANGLES EXERCISE - Self Assessment Test (Multiple Choise Questions)
34 Videos
Similar Questions
Show that in an A.P. the sum of the terms equidistant from the beginning and end is always same and equal to the sum of first and last terms.
View SolutionIn a finite GP the product of the terms equidistant from the beginning and end is always same and is equal to the product of first and last term.
View Solution
Knowledge Check
Statement -1: If a1,a2,a3,.....,an,... is an A.P. such that a1+a4+a7+....+a16=147, then a1+a6+a11=98
Statement -2: In an A.P., the sum of the terms equidistant from the beginning and the end is always same and is equal to the sum of first and last term.AStatement -1 is true, Statement -2 is True, Statement -2 is a correct explanation for Statement for Statement -1.BStatement -1 is true, Statement -2 is True, Statement -2 is not a correct explanation for Statement for Statement -1.CStatement -1 is true, Statement -2 is False.DStatement -1 is False, Statement -2 is True.
In a finite G.P. the product of the terms equidistant from the beginning and the end is always same and equal to the product of first and last term.
View SolutionIf n A.Ms are inserted between two numbers, prove that the sum of the means equidistant from the beginning and the end is constant.
View SolutionIn the expansion of (1+x)n the coefficients of terms equidistant from the beginning and the end are equal.
View SolutionThe first and the last terms of an A.P. are a and l respectively. Show that the sum of nth term from the beginning and nth term from the end is a+l.
View SolutionIn an A.P, the sum of first 2n terms is equal to the sum of next n terms. Then the ratio of the sum of first 3n terms to the next n terms is
View SolutionIf an A.P. consists of n terms with first term a and nth term l then show that the sum of the mth term from the beginning and the mth term from the end is (a+l).
View SolutionState 'T' for true and 'F' for false .
I. A sequence is an A.P ., if and only if the sum of its n terms is of the form An2+Bn , where A and B are constants .
II. If 18, a, b , −3 are in A.P., then a+b=15 .
III If a,c,b are in A.P., then 2c=a+b .
IV .The nth term from the end of an A.P. is the (m−n+1)th term from the beginning , where m terms are in A.P.
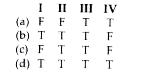
View Solution
