In an A.P. with first term 'a' and common difference 'd' t2n−tn is : (where tn is the nth term ) Solution in Tamil
nd
(2n−1)d
(n−1) d
a+nd
The correct Answer is:A
Step by step video, text & image solution for In an A.P. with first term 'a' and common difference 'd' t_(2n) - t_(n) is : (where t_(n) " is the " n^(th) term ) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NUMBERS AND SEQUENCESBOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - ACTIVITIES
9 Videos
- MENSURATIONBOOK - PREMIERS PUBLISHERSCHAPTER - MENSURATIONEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
16 Videos
- RELATIONS AND FUNCTION BOOK - PREMIERS PUBLISHERSCHAPTER - RELATIONS AND FUNCTION EXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
25 Videos
Similar Questions
This activity helps you to find H.C.F. of two positive numbers. We first observe the following instructions.
Construct a rectangle whose length and breadth are the given numbers.
View SolutionMatch the following:
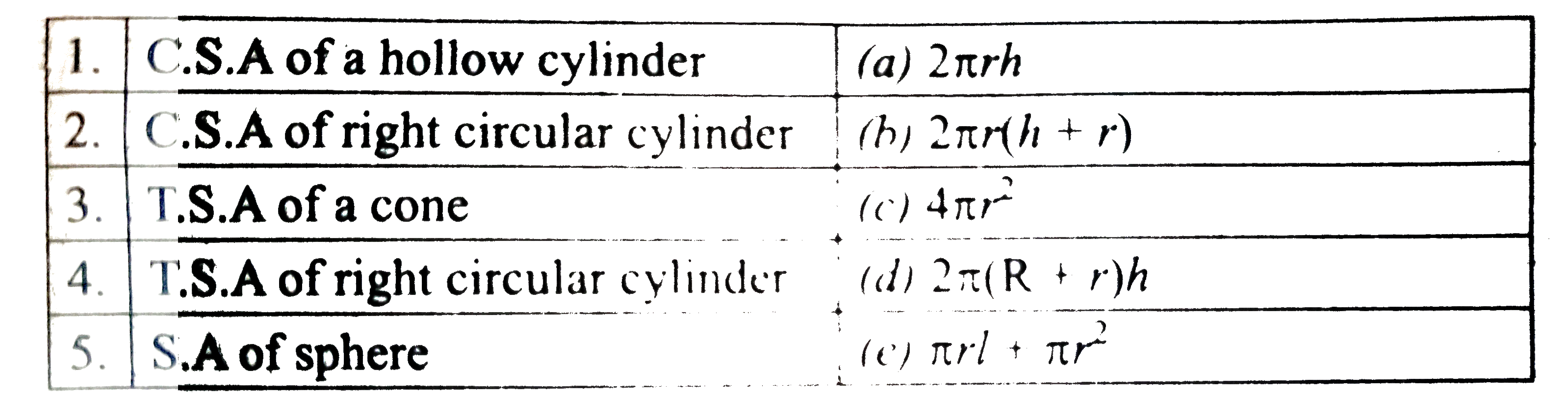
View SolutionIf n(A×B)=24andA={1,3,5,7}then n (B) is
View SolutionLet T_(r) be the r^(th) term of an A.P whose first term is a and common difference is d IF for some integer m,n,T_(m)=(1)/(n) and T_(n)=(1)/(m) then a-d=
View SolutionThe absolute value of the sum of first 20 terms of series, if Sn=n+12 and Tn−1Tn=1n2−1, where n is odd, given Sn and Tn denotes sum of first n terms and nth terms of the series
View Solutionकिसी A.P. का n वाँ पद tn हैं । तब दर्शायें कि tm+t2n+m=2tm+n.
View SolutionFind the first four terms of an A.P. whose first term is −3 and common difference −4, and also find tn.
View Solutionकिसी गु० श्रे० का सार्व अनुपात r है एवं tn n वां पद है। सिद्ध करें की (t1+t2+t3+...+tn):(tn+1+tn+2+tn+3+...+t2n)=1:rn.
View SolutionA sequence is defined as: tn+1=tn−tn−1 , where tn denotes the nth term of the sequence. If t1=1 and t2=5, find the sum of the first 100 terms of the above sequence.
View SolutionLet tp be the p th term of an A.P. if its n th tem is zero, show that t1+t3+t5+...+ to n th term=0.
View SolutionIf T54 is an fifty fourth term of an Arithmetic Progression is 61 and T4 is fourth term of an same Arithmetic progression is 64, then T10 of that series will be : (Tn=nth term of an A.P.)
View SolutionIf T54 is an fifty fourth term of an Arithmetic Progression is −61 and T4 is fourth term of an same Arithmetic progression is 64, then T10 of that series will be (Tn=nth term of an A.P.)
View SolutionIf tn is the nth term of an A.P. then the value of tn+1−tn−1 is ……
View SolutionIf tn is the nth term of an A.P., then t2n−tn is …..
View SolutionThe ratio of sum of m terms to the sum of n terms on an A.P is m2:n2 .If Tk is the Kth term, then T5T2 is
(A) 6
(B) 5
(C) 4
(D) 3
View Solution
