In an equilateral triangle prove that the centroid and the centre of the circumcircle (circumcentre) coincide.
The point of intersection of the medians of a triangle is called its centroid. The centroid of a triangle is the point located at 23 of the distance from a vertex along a median. The center of the circumcircle of this triangle is called the circumcentre.
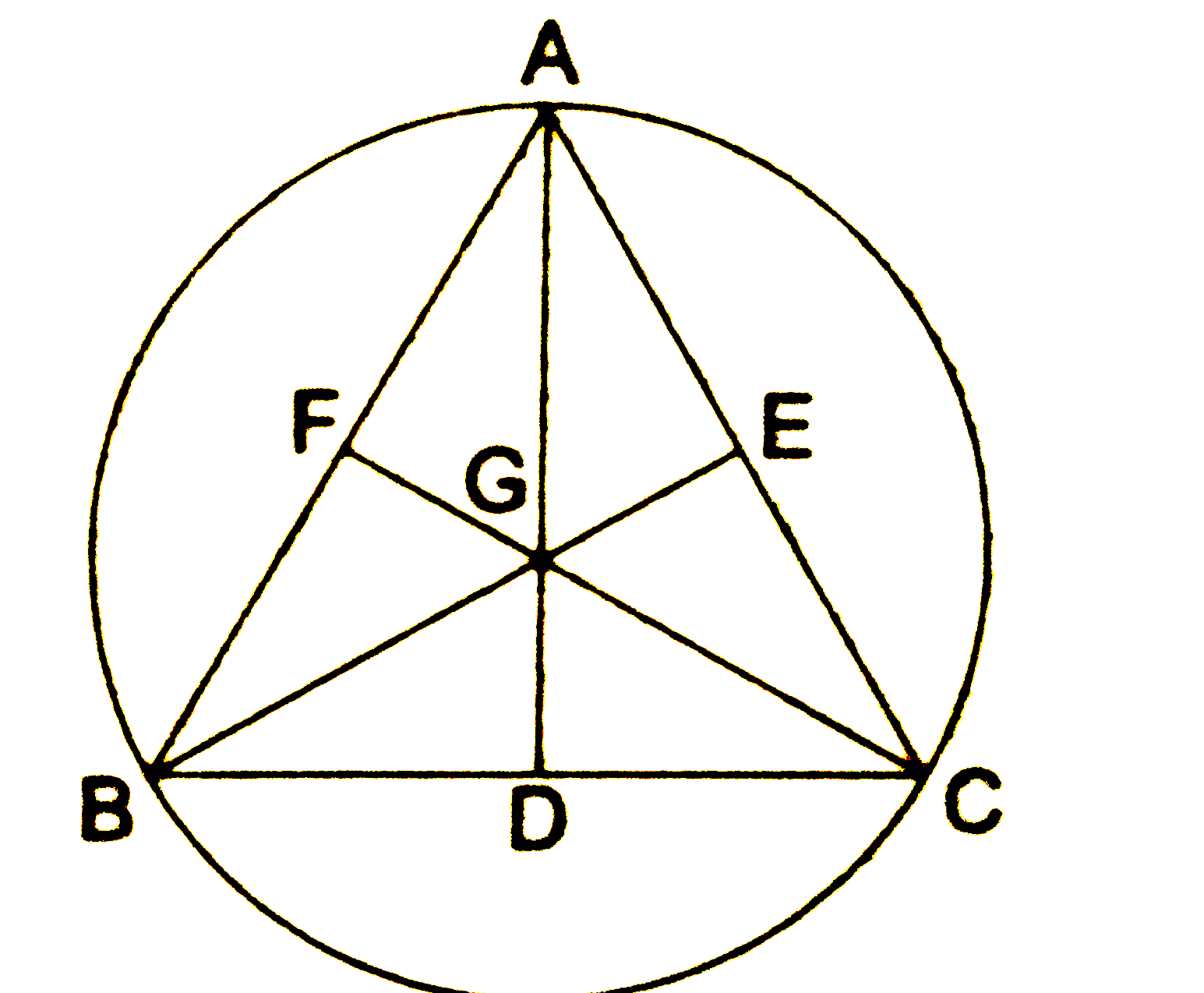
Let ΔABC be the given equilateral triangle and let its medians AD,BE and CF intersect at G.
Then G is the centroid of ΔABC.
In ΔBCE and ΔCBF we have
BC = CB [common]
∠B=∠C[ each equal to 60∘]
CE=BE[AC=AB⇒12AC=12AB]
∴ΔABC=CF
Similarly, AD=BE.
Thus, AD=BE=CF⇒23AC=12AB]
⇒GA=GB=GC
This shows that G is the circumcentre of ΔABC
Hence, G is the centroid as well as circumcentre of ΔABC.
Similar Questions
In an equilateral triangle, prove that the centroid and the circumcentre coincide.
View SolutionIn an equilateral triangle, prove that the centroid and centre of the circum-circle (circum centre) coincide) Given : An equilateral triangle ABC in which D, E and F are the mid-points of sides BC, CA and AB respectively. To Prove: The centroid and circum centre are coincident. Construction : Draw medians AD, BE and CF
View Solution
Knowledge Check
In an equilateral triangle, the incentre, circumcentre, orthocentre and centroid are :
AcollinearBconcyclicCcoincideDnone of theseIn an equilateral triangle, the incentre, circumcentre, orthocentre and centroid are :
AconcylicBcoincidentCcollinearDnone of theseIn an equilateral triangle, the inradius, circumradius, and one of the exradii are in the ratio
AconcylicBcoincidentCcollinearDnone of these
From the figure, ABC is an equilateral triangle of side 14cm. M is the center of the circumcircle. Find the area of shaded resin.
View SolutionThe controid of an equilateral triangles is (0,0) and the length of the altitude is 6. The equation of the circumcircle of the triangle is
View SolutionIf the centroid of an equilateral triangle is (1,1) and its one vertex is (−1,2) then the equation of the circumcircle is
View Solution(-1,2) is the vertex of an equilateral triangle whose centroid is (1, 1), then the equation of its circumcircle is
View SolutionThe height of an equilateral triangle is 4√3cm. The ratio of the area of its circumcircle to that of its in-circle is
View Solution
