In an isoceles triangle OAB , O is the origin and OA=OB=6 . The equation of the side AB is x-y+1=0 Then the area of the triangle is
2√21
√142
√1422
√712
The correct Answer is:D
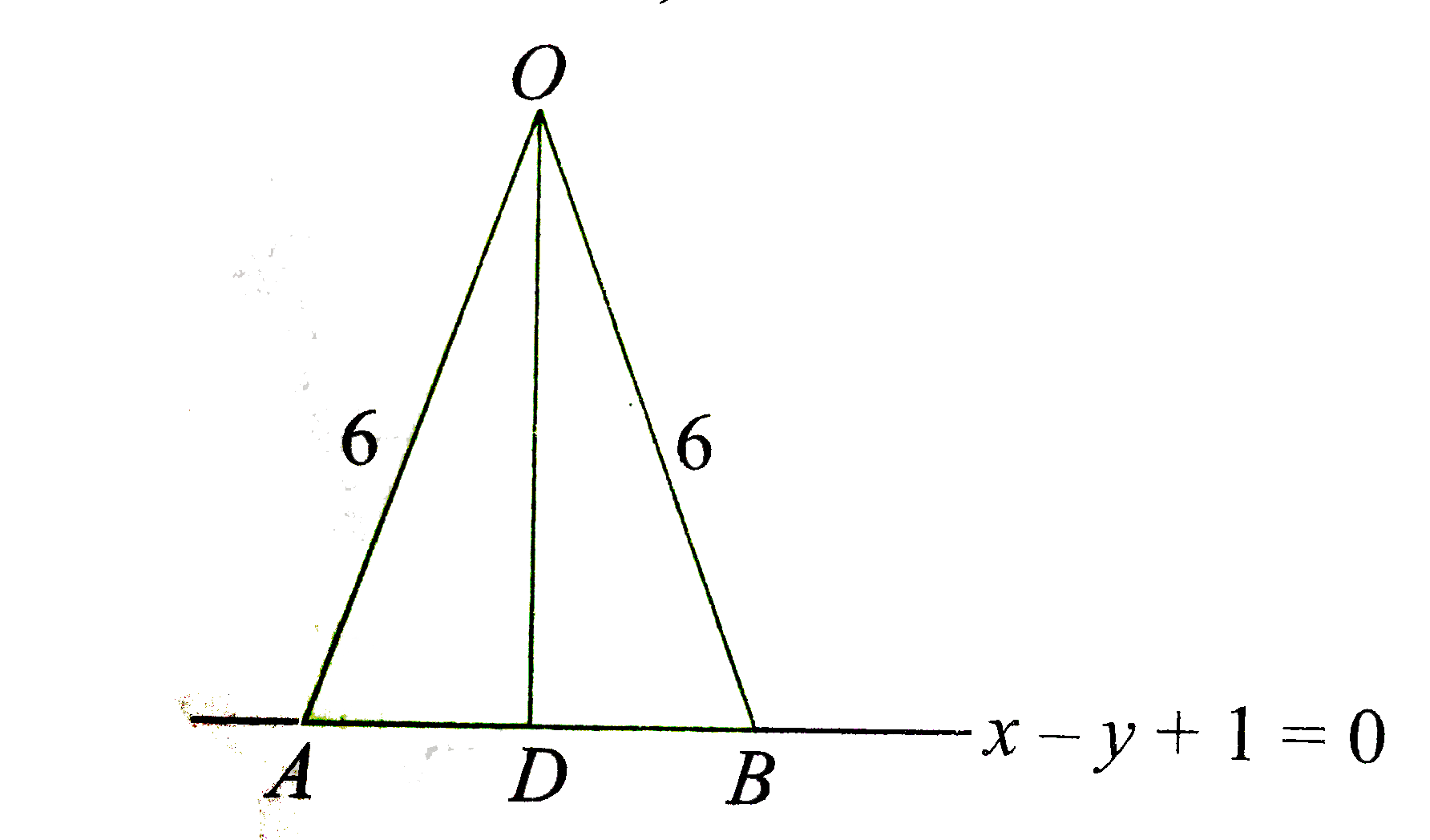
Let D be the midpoint of AB.
OD=1√2
AD=√62−OD2=√36−12=√172
∴Area of triangle=12×AB×OD=√172×√12=√712
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
The equation of two equal sides AB and AC of an isosceies triangle ABC are x+y=5 and 7x−y=3respectively Find the equations of the side BC if the area of the triangle ofABC is 5 units
View SolutionTriangle OAB is isosceles right triangle right angled at O.O is origin and equation of AB is 2x+3y=6 then area of triangle OAB is 3613 b. 1217 c. 135 d. 1713
View Solution
Knowledge Check
The equations of two equal sides AB and AC of an isosceles triangle ABC are x + y = 5 and 7x - y = 3 respectively. What will be the equation of the side BC if area of triangle ABC is 5 square units.
Ax + 3y - 1 = 0Bx - 3y + 1 = 0C2x - y = 5Dx + 2y = 5The line x + y = p meets the axis of x and y at A and B respectively. A triangle APQ is inscribed in the triangle OAB, O being the origin, with right angle at Q, P and Q lie respectively on OB and AB. If the area of the triangle APQ is 3/8th of the area of the triangle OAB, then AQBQ is equal to
A2B2/3C1/3D3
If a vertex of an equilateral triangle is the origin and the side opposite to it has the equation x+y=1, then orthocentre of the triangle is :
View SolutionThe line x+y=a meets the axes of x and y at A and B respectively. A triangle AMN is inscribed in the triangle OAB, O being the origin, with right angle at N, M and N lie respectively on OB and AB. If the area of the triangle AMN is 38 of the area of the triangle OAB, then ANBM is equal to:
View SolutionThe perimeter of an isoceles triangle is 544 cm and its equal sides is 5/6 times of its base then the area of triangle (in cm2) is-
View SolutionLet ABC be a triangle with equations of the sides AB,BCandCA respectively x−2=0,y−5=0and5x+2y−10=0. Then the orthocentre of the triangle lies on the line
View SolutionΔOAB is formed by the lines x2−4xy+y2=0 and the line AB. The equation of line AB is 2x+3y−1=0.Find the equation of the median of the triangle drawn from the origin.
View Solution(1)A triangle formed by the lines x+y=0,x−y=0 and lx+my=1. If land m vary subject to the condition l2+m2=1 then the locus of the circumcentre of triangle is: (2)The line x+y=p meets the x-axis and y-axis at A and B, respectively. A triangle APQ is inscribed in triangle OAB,O being the origin, with right angle at Q.P and Q lie, respectively, on OB and AB. If the area of triangle APQ is 38th of the area of triangle OAB, then AQBQ is: equal to
View Solution
