In an isosceles triangle ABC with AB=AC,BD is perpendicular from B to the side AC. Prove BD2−CD2=2CD.AD.
GIVEN AΔABC in which AB=BCandBD⊥AC.
PROOF From fight ΔABD, we have
AB2=AD2+BD2 [ by Puthagora's theorem]
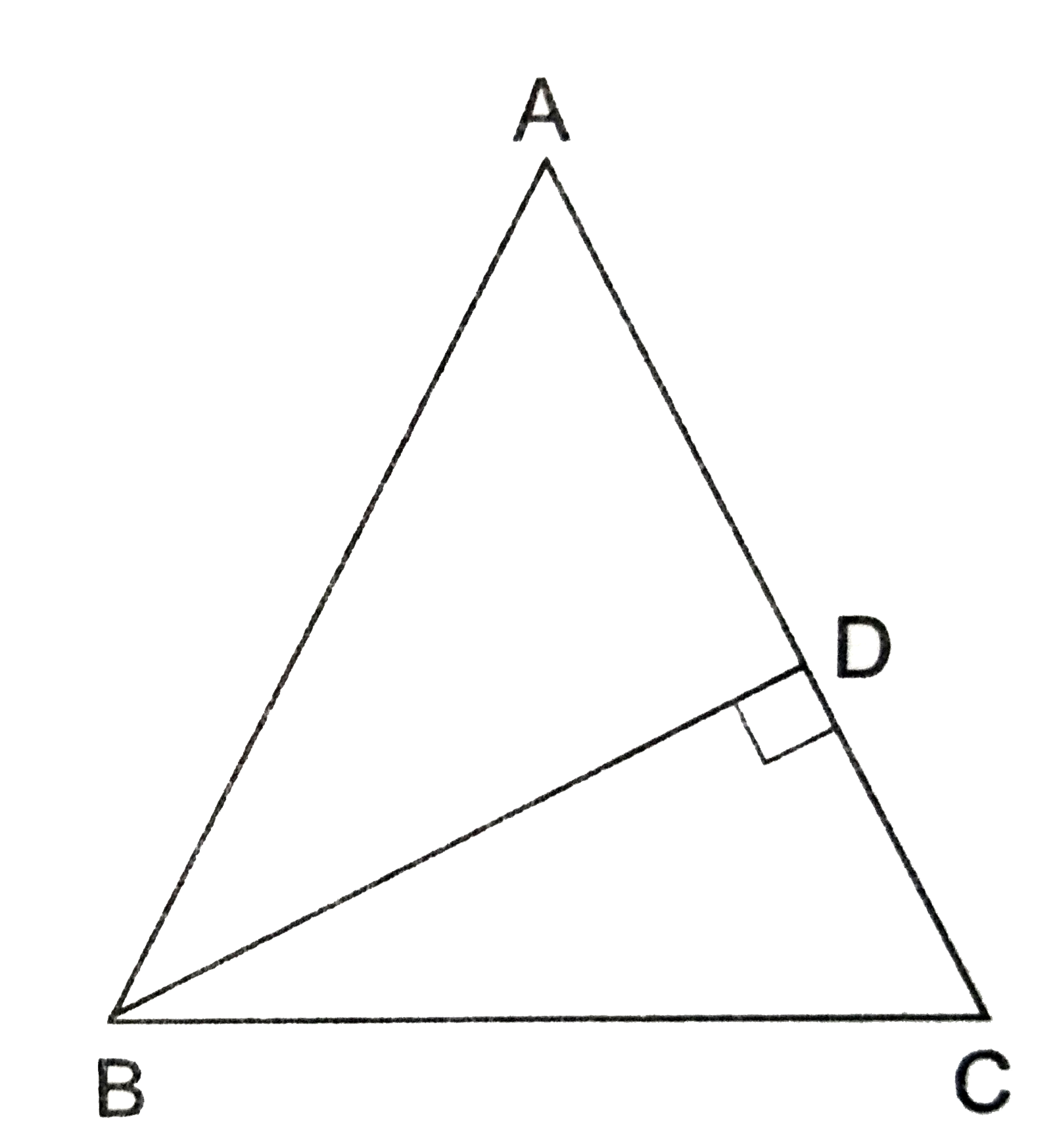
⇒AC2=D2+BD2[∴AB=AC]
⇒(CD+AD)2=AD+BD2[∴AC=CD+AD]
⇒CD2+AD2+2CD⋅AD=AD2+BD2
⇒(BD2−CD2)=2CD⋅AD.
Hence, (BD2−CD2)=2CD⋅AD
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
In an isosceles triangle ABC with AB=AC , BD is perpendicular from B to the side AC . Prove that BD2−CD2=2 CDAD
View SolutionIn an isosceles triangle ABC with AB = AC, BD is perpendicular from B to side AC. Prove that BD2−CD2=2CD.AD
View SolutionΔABC is an isosceles triangle. AB = AC and BD is perpendicular on AC from vertex B, then BD2−CD2 is equal to-
View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
AB2−BD2=AC2−CD2
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
View SolutionIn Figure, ABC is an isosceles triangle with AB=AC, BD and CE are two medians of the triangle. Prove that BD=CE
View SolutionABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
View SolutionIf ABC is an isosceles triangle with AB=AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionIf ABC is an isosceles triangle with AB=AC . Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionABC is an isosceles triangle with AB =AC and BD,CE are its two medians. Show that BD=CE .
View Solution
