In ∠ABC and ∠LMN, AB = LM and BC = MN. Which of the following conditions can make the two triangles congruent ?
∠A=∠L
∠B=∠M
∠C=∠N
All of these
The correct Answer is:B
To determine the conditions under which triangles △ABC and △LMN can be congruent, we can follow these steps:
1. Identify Given Information:
- We know that AB=LM and BC=MN.
- These represent two sides of each triangle.
2. Draw the Triangles:
- Draw triangle ABC with sides AB and BC.
- Draw triangle LMN with sides LM and MN.
3. List the Known Sides:
- From the problem, we have:
- AB=LM (first side)
- BC=MN (second side)
4. Determine the Missing Information:
- To establish congruence between two triangles, we need to know about the angles as well.
- We already have two sides, but we need to find the angle that is included between these two sides.
5. Identify the Angle:
- The angle that is included between the sides AB and BC in triangle ABC is angle B.
- Similarly, the angle included between sides LM and MN in triangle LMN is angle M.
6. Set Up the Congruence Condition:
- For the triangles to be congruent, we need:
- AB=LM
- BC=MN
- ∠B=∠M
7. Apply the SAS Congruence Criterion:
- The condition we have is two sides and the included angle (SAS).
- Therefore, by the SAS (Side-Angle-Side) criterion, we can conclude that:
△ABC≅△LMN
Conclusion:
The condition that can make the two triangles congruent is:
- ∠B=∠M.
- We know that AB=LM and BC=MN.
- These represent two sides of each triangle.
- Draw triangle ABC with sides AB and BC.
- Draw triangle LMN with sides LM and MN.
- From the problem, we have:
- AB=LM (first side)
- BC=MN (second side)
- To establish congruence between two triangles, we need to know about the angles as well.
- We already have two sides, but we need to find the angle that is included between these two sides.
- The angle that is included between the sides AB and BC in triangle ABC is angle B.
- Similarly, the angle included between sides LM and MN in triangle LMN is angle M.
- For the triangles to be congruent, we need:
- AB=LM
- BC=MN
- ∠B=∠M
- The condition we have is two sides and the included angle (SAS).
- Therefore, by the SAS (Side-Angle-Side) criterion, we can conclude that:
△ABC≅△LMN
The condition that can make the two triangles congruent is:
- ∠B=∠M.
Topper's Solved these Questions
- IMO QOESTION PAPER 2017-18 SET-BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QOESTION PAPER 2017-18 SET-BEXERCISE - EVERYDAY MATHEMATICS
10 Videos
- IMO MODEL TEST PAPER 2 BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO MODEL TEST PAPER 2 EXERCISE - Achievers Section
5 Videos
- IMO QUESTION PAPER 2017-18 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017-18 SET AEXERCISE - ACHIEVERS SECTION
5 Videos
Similar Questions
Knowledge Check
Which of the following is false for two congruent triangles?
ACorresponding angles are equalBTwo sides and included angles are equalCCorresponding sides are equalDTwo angles and one side are equalWhich of the following triangles is congruent to the given triangle?
 A
A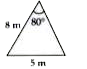 B
B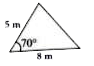 C
C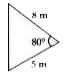 D
D
In ΔPQRandΔABC, ∠Q=∠B=90∘,PQ=AB,andQR=BC. Which of the following property can be used to prove the congruence of ΔPQR and ΔABC ?
ASSSBRHSCASADSAS
State the condition by which the following pairs of triangles are congruent.
View SolutionBy which congruency criterion, the two triangles in Figure are congruent?
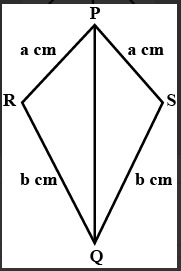
View SolutionIn ΔPQRandΔABC, ∠Q=∠B=90∘,PQ=AB,andQR=BC. Which of the following property can be used to prove the congruence of ΔPQR and ΔABC ?
View SolutionWhich of the following pairs of triangles is congruent?
View SolutionIf in two triangles ABC and PQR, ABQR=BCPR , then which of the following is true?
View Solution
