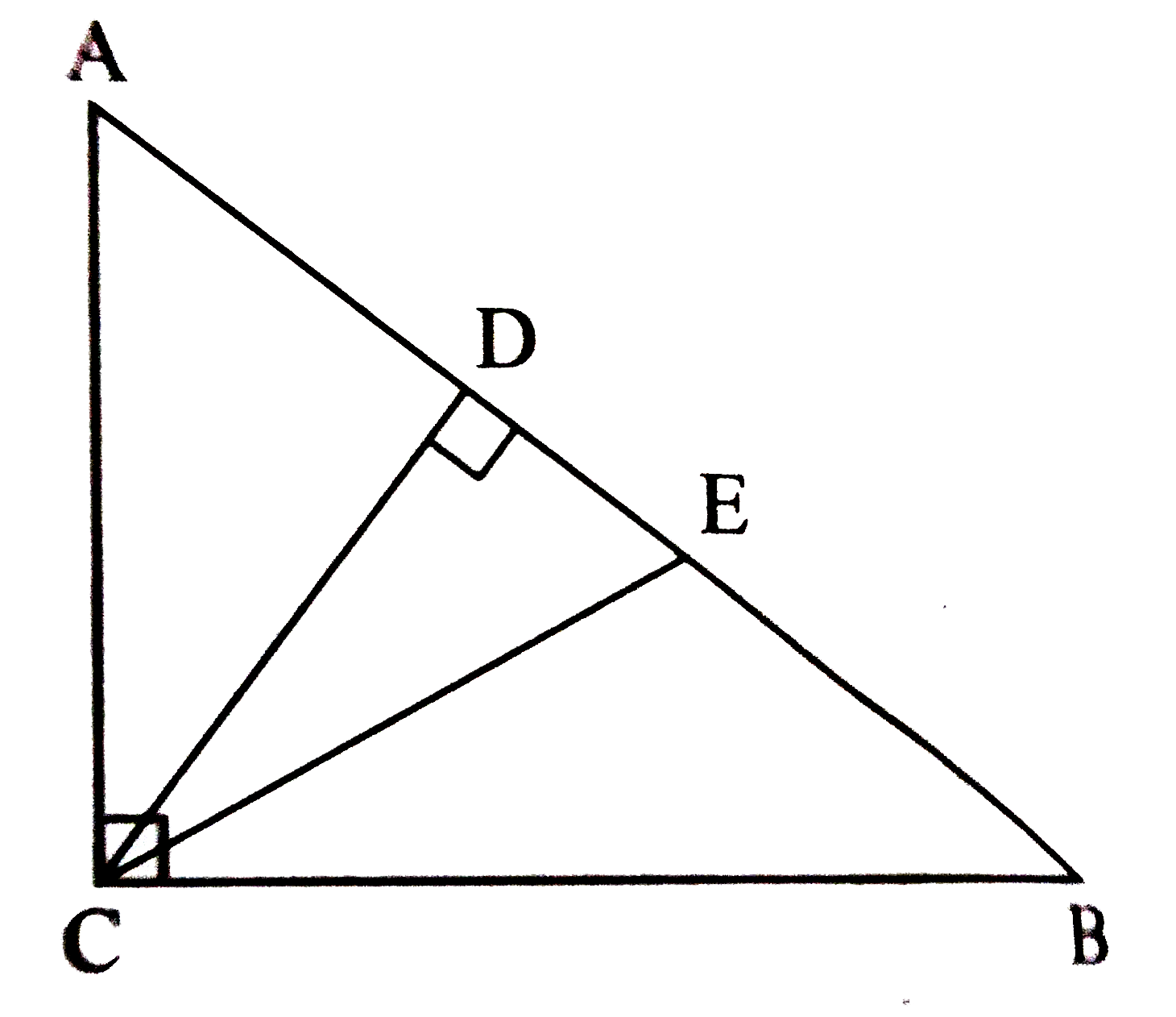
In ΔABC,∠ACB=90∘, seg CD⊥ side AB and seg CE is angle bisector of ∠ACB
Prove : ADBD=AE2BE2
Video Solution
Text Solution
In ΔACB,
ray CE bisects ∠ACB
∴ by theorem of angle bisector of a Delta
ACCB=AEEB
Squaring both the sides , we get ,
AC2CB2=AE2EB2
In ΔACB,∠ACB=90∘
seg CD ⊥ hypotenuse AB
ΔACB~ΔADC~ΔCDB
... (Similarity of right angled Delta ) ... (2)
ΔACB~ΔADC ... [ From (2)]
ACAD=ABAC (Corresponding sides of similar triangfle )
∴AC2=AB×AD ...(3)
also, ΔACB~ΔCDB ... [ From (2)]
∴ABBC=BCBD ( Correesponding sides of similar Delta )
∴BC2=AB×BD ... (4)
Substituting the values of (3) and (4) in (1) , we get
AB×ADAB×BD=AE2EB2
∴ADBD=AE2EB2
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE )7videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Choose the correct alternative :3videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONS EXERCISE - EXAMPLE FOR PRACTICE22videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions10videos
CIRCLE
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔABC,∠B=90∘ and BD⊥AC. If AC = 9 cm and AD = 3 cm, then BD is equal to :
A2√2 cmB3√2 cmC2√3 cmD3√3 cm - Question 2 - Select One
In a △ABC. AB = 5 cm, AC = 7 cm. If AD is the angle bisector of angle A, then BD :CD is :
A25:49B49:25C6:1D5:7 - Question 3 - Select One
In andsegBD bot sACandAD=DC then ……..
ABD2=DC×ACBBD2=AD×ACCBD2=DC×ACDnone of these
In a ΔABC,∠B=100∘,∠C=70∘,AE⊥BC&AD is angle bisector . Find ∠EAD .
View SolutionIn a ΔABC,∠B=100∘,∠C=70∘,AE⊥BC&AD is angle bisector . Find ∠EAD .
View SolutionIn ΔABC,∠B=90∘andBD⊥AC.IfAC=9cmandAD=3 cm then BD is equal to
View SolutionIn ΔABC,∠ACB=90∘
seg CD ⊥ seg AB
seg DE ⊥ seg CB.
Show that: CD2×AC=AD×AB×DE
 View Solution
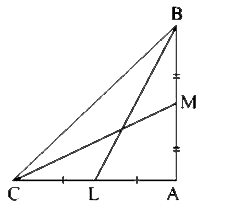
View SolutionIn ΔABC,∠BAC=90∘, seg BL and seg CM are median of ΔABC. Then prove that: 4(Bl2+Cm2)=5BC2
 View Solution
View Solution

