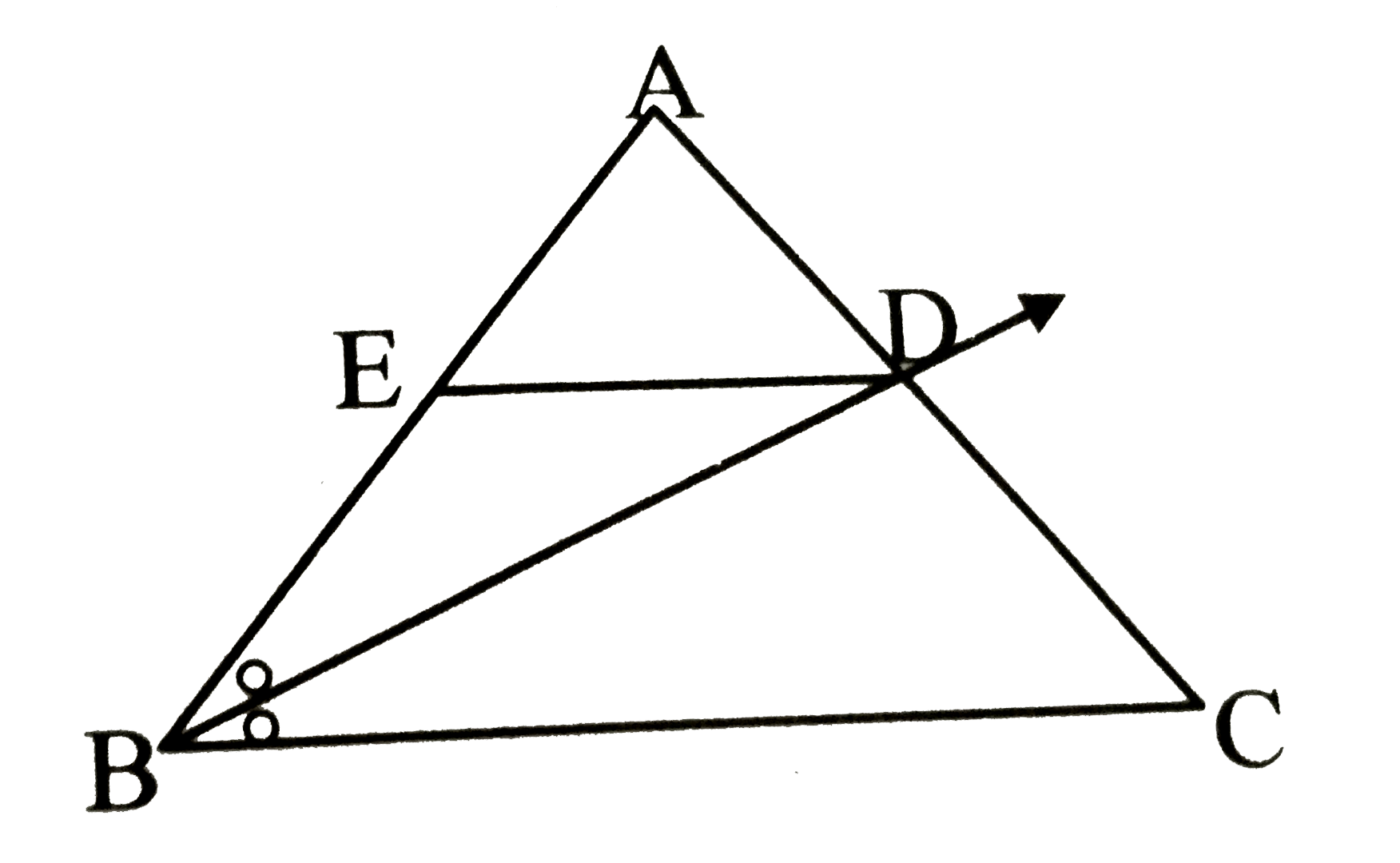
In , ray BD bisects . A-D-C, side DEside BC, A-E-B, then prove that .
The correct Answer is:
Step by step video & image solution for In Delta ABC, ray BD bisects angleABC. A-D-C, side DEabs()side BC, A-E-B, then prove that (AB)/(BC) = (AE)/(EB). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Try this
1 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Practice Set 1.1
8 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Chapter Assessment
19 Videos
- QUESTION FROM STD. IXBOOK - TARGET PUBLICATIONCHAPTER - QUESTION FROM STD. IXEXERCISE - Statistics
14 Videos
- STATISTICSBOOK - TARGET PUBLICATIONCHAPTER - STATISTICSEXERCISE - Problem Set-6
21 Videos
Similar Questions
In ΔABC, ray BD bisects ∠ABC. A−D−C, side DE∣∣ side BC, A−E−B.
Prove that, ABBC=AEEB.
Complete the activity by filling the boxes.
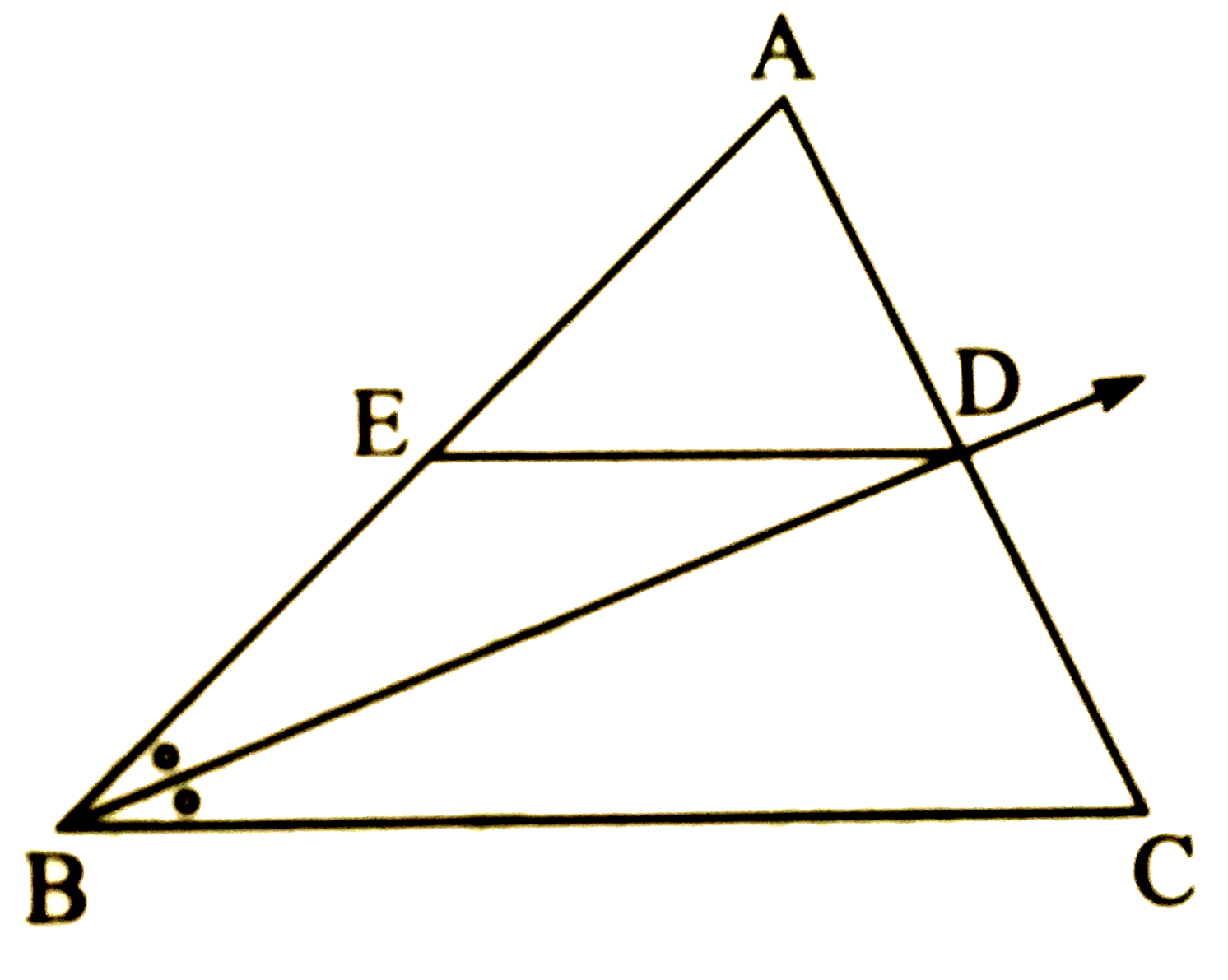
In ΔABC, ray BD is the bisector of ∠ABC
∴ABBC=□.......(I) (By angle bisector theorem)
In ΔABC, seg DE∣∣ side BC
∴AEEB=ADDC........(II) □
∴AB□=□EB.......[From (I) and (II)]
View SolutionIn ΔABC,ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB ≅seg AC, then prove that ED || BC.
View Solution
Knowledge Check
In ΔABC, D and E are two points on the sides AB and AC respectively so that DE || BC and ADBD=23. Then the area of trapezium DECBthe area of ΔABCequa to
A59B2125C145D514
ΔABC~ΔDEF, Prove that ABDE=AB+BC+ACDE+EF+DF
View SolutionIn a triangle ABC, D is midpoint of side BC. If AC>ABandAE⊥BC, then prove that AB2=AD2−BC.ED+14BC2
View SolutionIn ABC , ray AD bisects ∠A and intersects BC in D . If BC=a , AC=b and AB=c , prove that BD=acb+c (ii) D C = abb+c
View SolutionIf a line intersects sides AB and AC of a ΔABCat D and E respectively and is parallel to BC, prove that ADAB=AEAC
View SolutionIn ΔABC, the bisector of the angle A meets the sides BC at D and the circumscirbed circle at E. Prove that DE=a2sec.A22(b+c)
View SolutionIn ΔABC, D is the midpoint of side AB. Line DE∣∣ side BC. A−E−C. Prove that pont E is the midpoint of side AC.
View SolutionIn rectangle ABCD, E is the midpoint of side BC. Prove that, AE = DE.
View Solution
