Question

In $\Delta ABC$ , with usual notations prove that :
$b^2=c^2+a^2-2ca\cos B$.

Explanation

Consider that for `Delta ABC , angle B ` is in a standed
position i.e. vertex B is at the origin and the side BC
is along positive x-axis. As ` angle B ` is an angle of a triangle .
` therefore angle B ` can be acute or obtuse

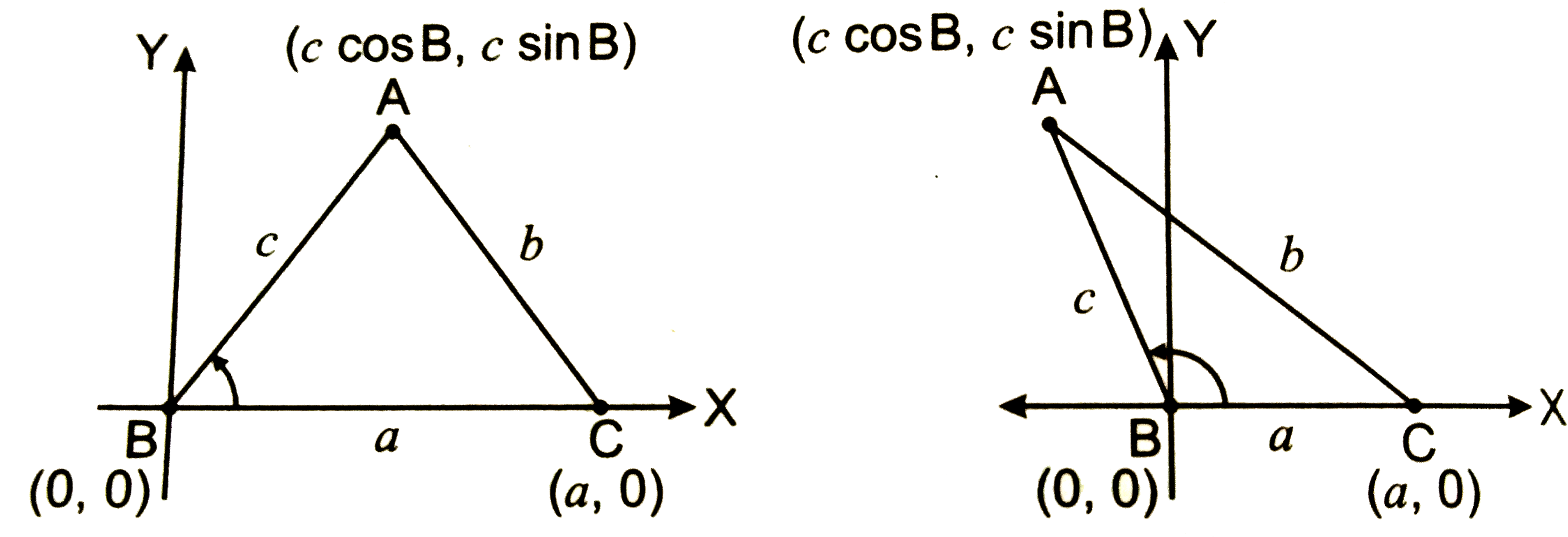
From cartesian co-ordinates of 1 and 2 we get .
` B -= (0,0) , A -= (c cos B , c sin B ) and C -= (a,0)`
Now consider `l (CA) = b `
` therefore l (CA)^(2) = b^(2)`
` therefore b^(2) = (a - c cos B)^(2) + (0 - c sin B)^(2)`
" " ... [By distance formula]
`= a^(2) - 2"ca cos " B + c^(2) cos^(2) B + c^(2) sin^(2) B `
` a^(2) - 2"ca cos "B + c^(2) (cos^(2) B + sin^(2) B)`
` a^(2) - 2ca cos B + c^(2)`
` therefore b^(2) = c^(2) + a^(2) - 2 "ca cos " B `