In and then
None of these
The correct Answer is:A
To solve the problem, we need to determine the relationship between the lengths of the sides of triangle PQR based on the angles given.
1. Identify the Angles:
- Angle P = 75°
- Angle Q = 35°
- Angle R = 70°
2. Determine the Largest Angle:
- Among the angles, 75° (Angle P) is the largest angle.
3. Apply the Triangle Inequality Theorem:
- The side opposite the largest angle is the longest side.
- Therefore, the side opposite Angle P (which is side QR) will be the longest side.
4. Identify the Sides Opposite Each Angle:
- Side QR is opposite Angle P (75°).
- Side PR is opposite Angle Q (35°).
- Side PQ is opposite Angle R (70°).
5. Rank the Sides Based on the Angles:
- Since QR is opposite the largest angle (75°), it is the longest side.
- The next largest angle is 70° (Angle R), which means side PQ is the second longest.
- The smallest angle is 35° (Angle Q), which means side PR is the shortest.
6. Conclusion:
- Based on the above reasoning, we can conclude that:
- QR > PQ > PR
Final Answer:
- Therefore, the correct relationship is that QR is the longest side, followed by PQ, and PR is the shortest side.
- Angle P = 75°
- Angle Q = 35°
- Angle R = 70°
- Among the angles, 75° (Angle P) is the largest angle.
- The side opposite the largest angle is the longest side.
- Therefore, the side opposite Angle P (which is side QR) will be the longest side.
- Side QR is opposite Angle P (75°).
- Side PR is opposite Angle Q (35°).
- Side PQ is opposite Angle R (70°).
- Since QR is opposite the largest angle (75°), it is the longest side.
- The next largest angle is 70° (Angle R), which means side PQ is the second longest.
- The smallest angle is 35° (Angle Q), which means side PR is the shortest.
- Based on the above reasoning, we can conclude that:
- QR > PQ > PR
- Therefore, the correct relationship is that QR is the longest side, followed by PQ, and PR is the shortest side.
Topper's Solved these Questions
- TRIANGLESBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - TRIANGLESEXERCISE - Achievers Section (HOTS) (Fill in the blanks.)
1 Videos
- TRIANGLESBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - TRIANGLESEXERCISE - Achievers Section (HOTS)
2 Videos
- SURFACE AREAS AND VOLUMESBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Achievers Section (HOTS)
3 Videos
Similar Questions
Knowledge Check
In ΔABC, if ∠A=60∘,∠B=50∘,and∠C=70∘, then find the longest side of the triangle ABC.
ABCBABCACDNone of these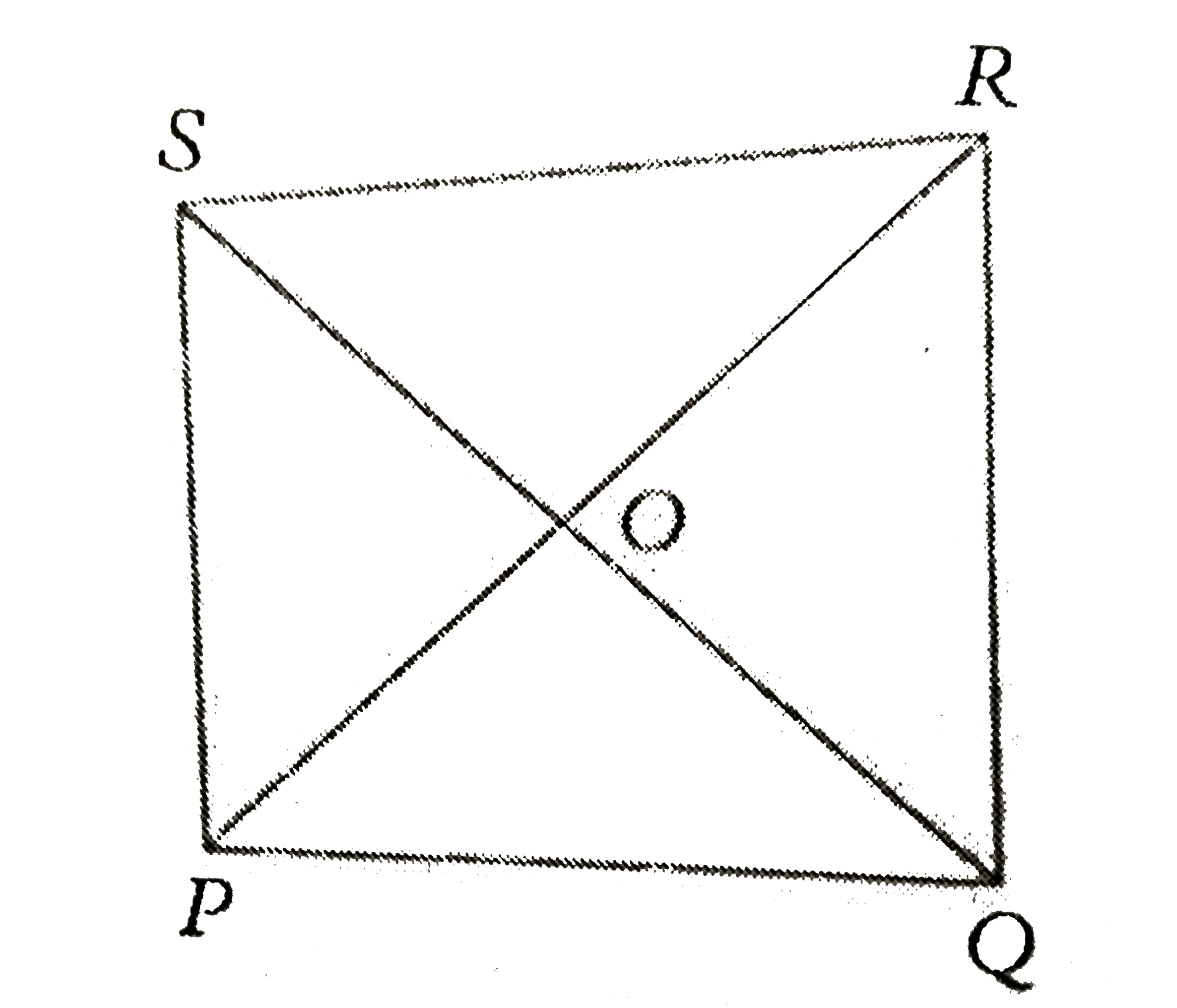
In the given figure, PQRS is a quadrilateral ,PR and QS intersect at O. If ∠PQR=70∘,∠SPQ=80∘,and∠PRQ=60∘, then find ∠SPR.A30∘B50∘C40∘D45∘If in a ΔABC,∠A=45∘,∠B=75∘, then
Aa+c√3=2bBa+c=2bCa+c√2=2bDa−c=2b
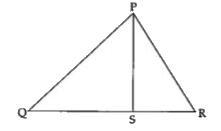
In ΔPQR it is given that = PQPR=QSSR. If ∠Q=70∘and∠R=50∘ then ∠QPS = ?
View SolutionIn a quadrilateral PQRS, ∠P = 50°, ∠Q = 50°, ∠R = 60°. Find ∠S. Is this quadrilateral convex or concave?
View SolutionConstruct a triangle PQR in which PQ= 2cm. ∠P=45∘,and∠Q=105∘.
View SolutionIn ΔPQR, If ∠R>∠Q, then
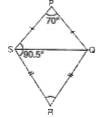
View SolutionPQRS is a kite. ∠P=70∘,∠S=90.5∘,∠R equals
View Solution
