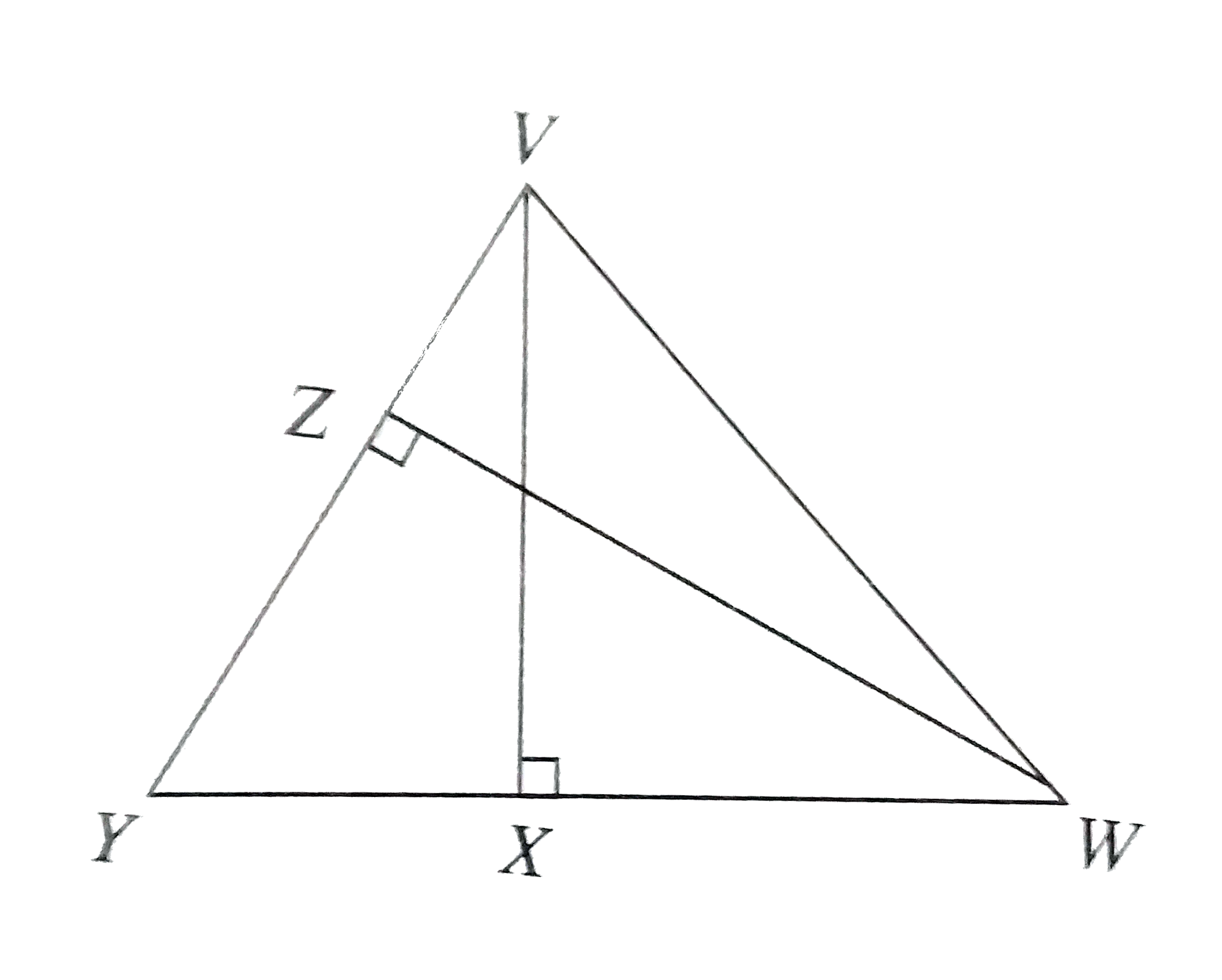
In ΔYVW in Figure, ¯¯¯¯¯¯VX is the altitude to side ¯¯¯¯¯¯¯YW, and ¯¯¯¯¯¯¯ZW is the altitude to side ¯¯¯¯¯¯YV. If ¯¯¯¯¯¯VX=3,¯¯¯¯¯¯YV=4, and ¯¯¯¯¯¯¯ZW=5, what is the length of side ¯¯¯¯¯¯¯YW ?
4.157
5.303
6.667
6.928
The correct Answer is:C
Put the given lengths into the figure :
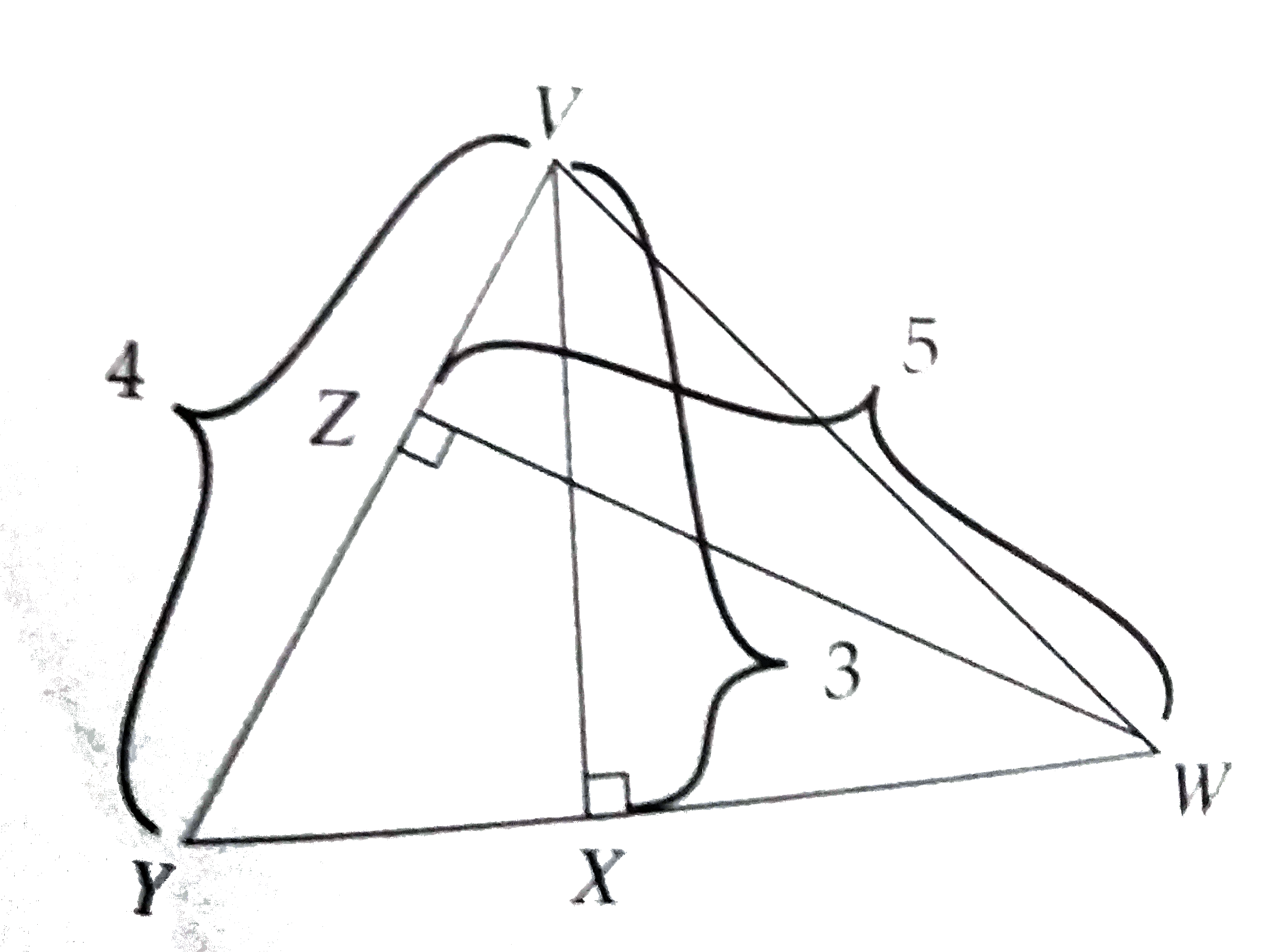
One - half the product of ¯¯¯¯¯¯¯YW and ¯¯¯¯¯¯VX is the same as one-half the product of ¯¯¯¯¯¯YV and ¯¯¯¯¯¯¯ZW . Or, ignoring the one - half, you can simply say that the products are equal.
12(¯¯¯¯¯¯¯YW)(¯¯¯¯¯¯VX)=12(¯¯¯¯¯¯YV)(¯¯¯¯¯¯¯ZW)
(¯¯¯¯¯¯¯YW)(¯¯¯¯¯¯VX)=(¯¯¯¯¯¯YV)(¯¯¯¯¯¯¯ZW)
(¯¯¯¯¯¯¯YW)(3)=(4)(5)
(¯¯¯¯¯¯¯YW)=203≈6.667
Topper's Solved these Questions
- PLANE GEOMETRY BOOK - KAPLANCHAPTER - PLANE GEOMETRY EXERCISE - PLANE GEOMETRY FOLLOW - UP TEST
6 Videos
- MISCELLANEOUS TOPICS BOOK - KAPLANCHAPTER - MISCELLANEOUS TOPICS EXERCISE - MISCELLANEOUS TOPICS FOLLOW - UP TEST
12 Videos
- PRACTICE TEST 1 BOOK - KAPLANCHAPTER - PRACTICE TEST 1 EXERCISE - PRACTICE TEST
50 Videos
Similar Questions
Knowledge Check
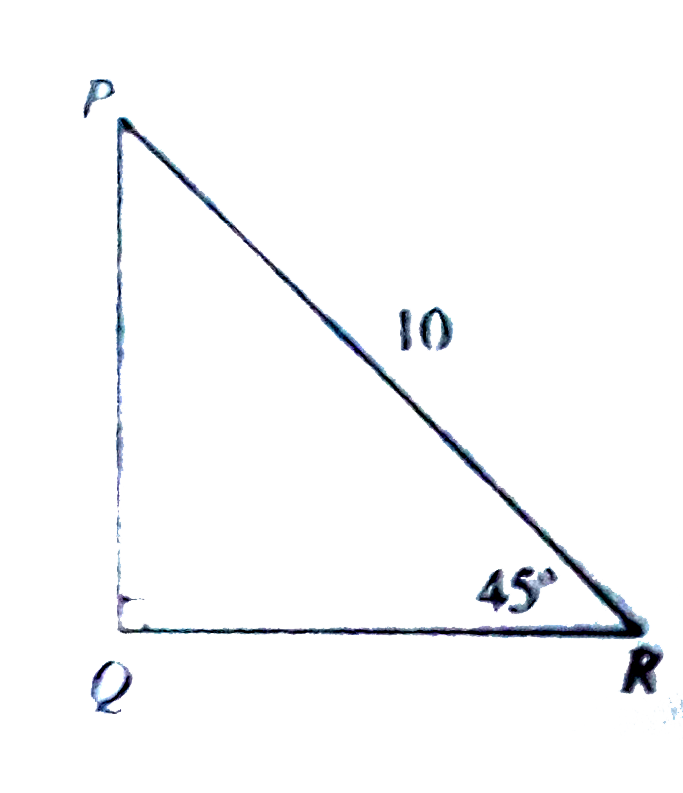
What is the length of ¯¯¯¯¯¯QR ?A5B5√22C10√2D5√2
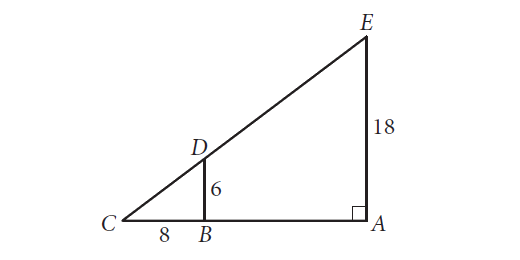
In the figure above, ¯¯¯¯¯¯BD is parallel to ¯¯¯¯¯¯AE. What is the length of ¯¯¯¯¯¯CE ?
View SolutionThe length of ¯¯¯¯¯¯¯WZ is 3a+15, and the length of ¯¯¯¯¯¯¯WX is 7a+5. If Y is the midpoint of ¯¯¯¯¯¯XZ, what is the length of ¯¯¯¯¯¯¯WY ?
View SolutionMagnetic length of a bar magnet is
View SolutionX, Y, and Z all lie on a number line. Segment ¯¯¯¯¯¯XY has a length of 5 and ¯¯¯¯¯¯YZ has a length of 7. If point U is the midpoint of ¯¯¯¯¯¯XZ,and¯¯¯¯¯¯UZ>2, what is the length of ¯¯¯¯¯¯UZ?
View SolutionIf the midpoints of segments ¯¯¯¯¯¯¯GH,¯¯¯¯¯¯JK,¯¯¯¯¯¯¯LM are connected, what is the area of the resulting triangle ?

View SolutionThe ratio of ¯¯¯¯¯¯DB to ¯¯¯¯¯¯EF is 4 to 9. If ¯¯¯¯¯¯DF=2, what is the distance from D to the midpont of ¯¯¯¯¯¯EF ?
View Solution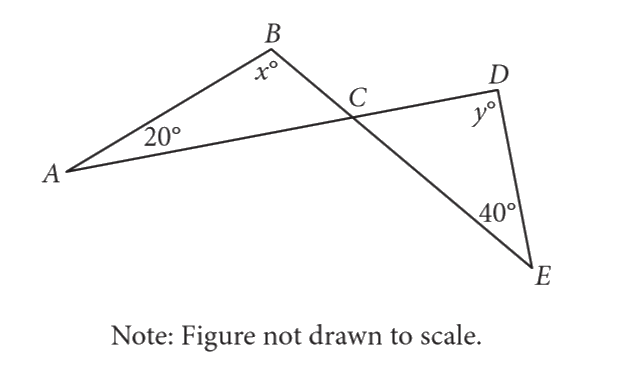
In the figure above, ¯¯¯¯¯¯AD intersects ¯¯¯¯¯¯BE at C. If x = 100, what is the value of y ?
View Solution