In ΔABC, E is the midpoint of the median AD. BE produced meets AC at F. Prove that AF=(13)AC
GIVEN A ΔABC in which AD is a median and E is the midpoint of AD. Also, BE is produiced to meet AC at F.
TO PROVE AF=13AC.
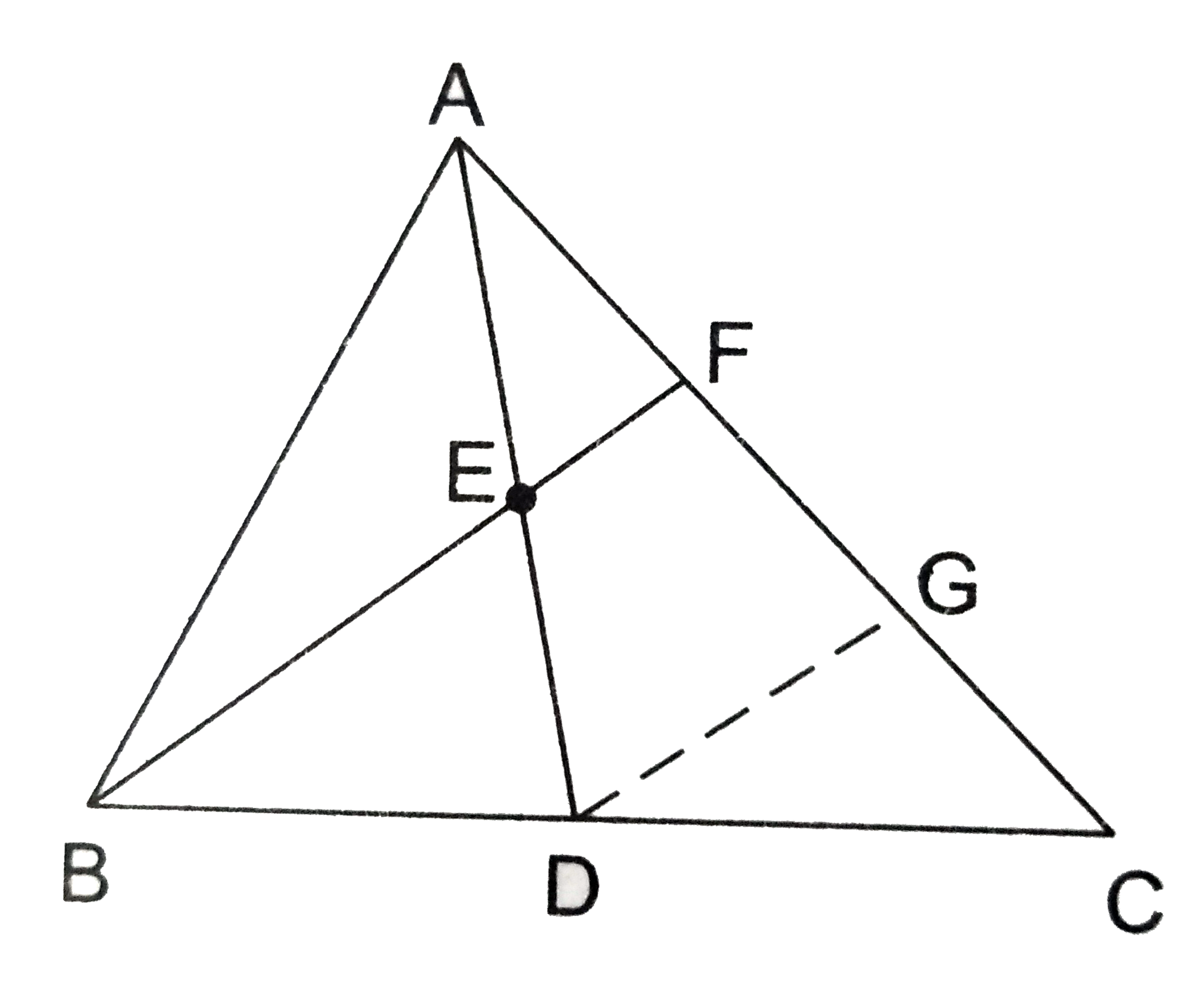
CONSTRUCTIO From D, draw DG||EF, meeting AC at G.
PROOF In ΔBCF. D is the midpoint of BC and DG||BF.
∴G is the midpoint of CF.
So, FG=GC.
Thus, AF=FG=GC.
∴AC=(AF+FG+GC)=3AF
Hence, AF=13AC
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
E is a mid-point of median AD of ΔABC. BE is extended to meet AC at F. In what ratio AC is divided by F.
A2:3B2:1C1:3D3:2
In the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.

View SolutionIn a triangle ABC, AD is the median through A and E is the midpoint of AD, and BE produced meets AC at F. Then AF is equal to
View SolutionIn a ΔABC,BD is the median to the side Ac, BD is produced to E such that BD = DE. Prove that AE is parallel to BC.
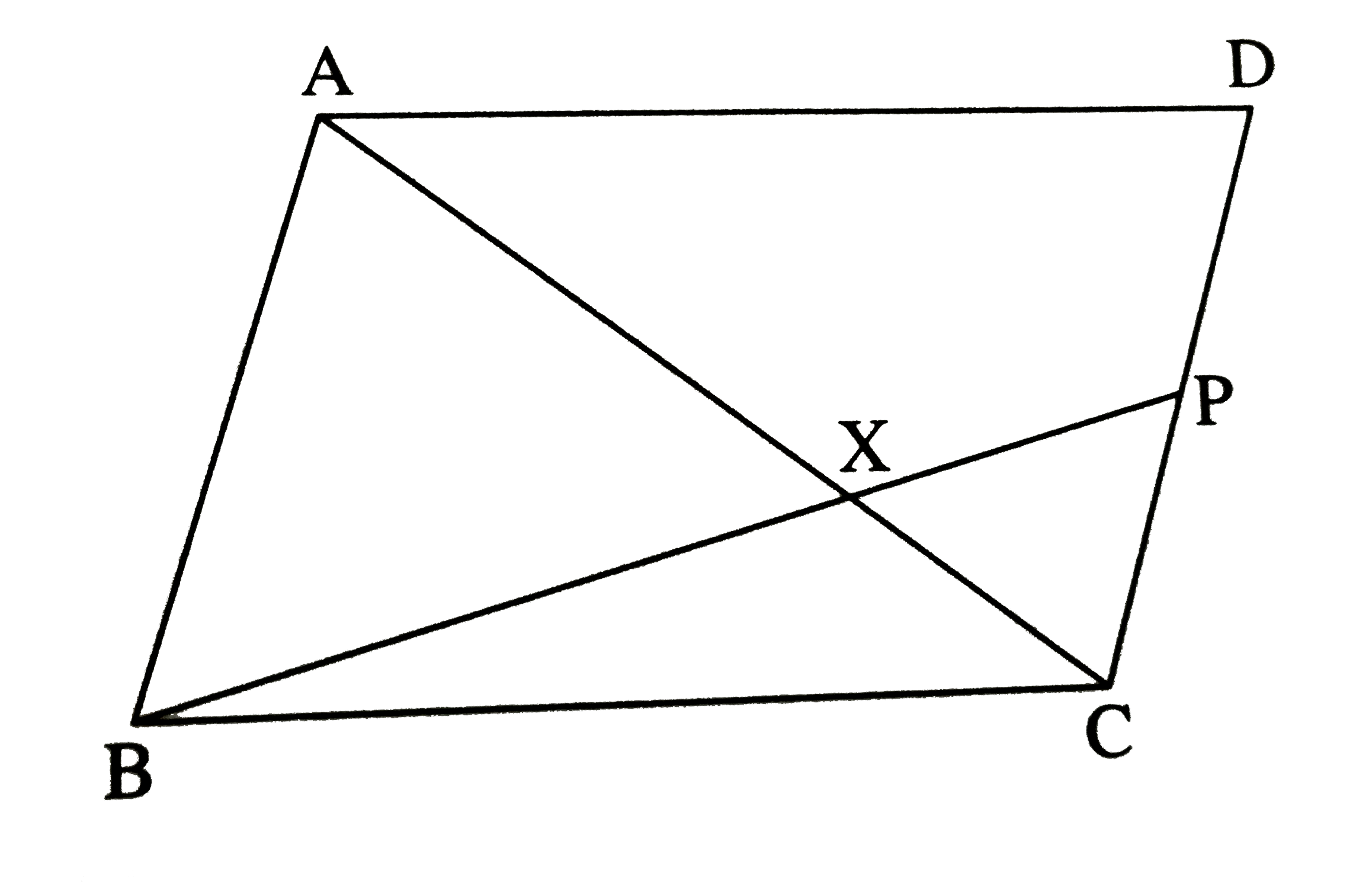
View Solution□ABCD is a parallelogram. P is the midpoint of side CD. Seg BP meets diagonal AC at X. Prove that 3AX=2AC.
View SolutionIn ΔABC,D is the mid-pointpoint of BC and E is mid-point of AD.BE is produced to meet the side AC in F.Then BF is equal to
View SolutionE is the mid-point of the median AD of ΔABC. Line segment BE meets AC at point F when produce, prove that AF=13AC.
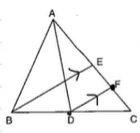
View SolutionIn Figure, AD, and BE are medians of ABC and BE∣∣DF. Prove that CF=14AC.
View Solution
