Question

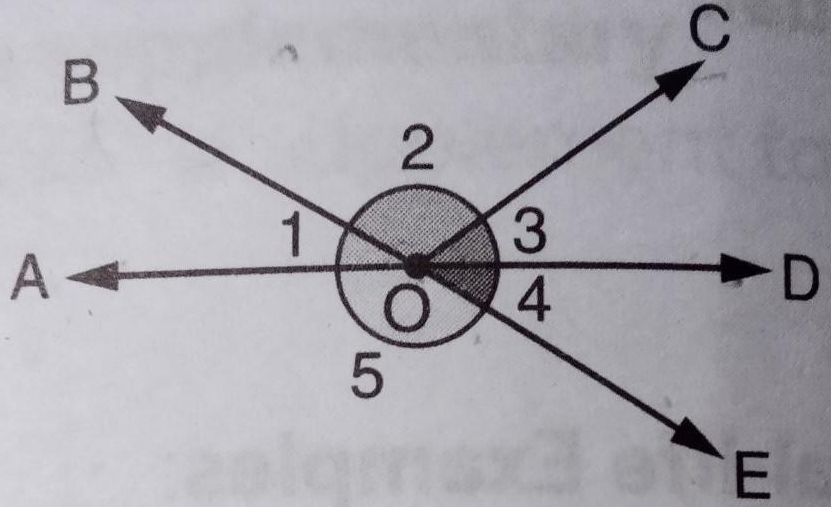
In Fig. 15, write down:
(i) each linear pair (ii) each pair of vertically opposite angles.

Explanation

To solve the problem, we need to identify the linear pairs and vertically opposite angles in the given figure (Fig. 15). Let's go through the steps systematically.

Step 1: Identify Linear Pairs

A linear pair consists of two adjacent angles formed when two lines intersect. The sum of the angles in a linear pair is always 180 degrees.

1. Angle 1 and Angle 2: These angles are adjacent and form a linear pair.
2. Angle 2 and Angle 4: These angles are adjacent and form another linear pair.
3. Angle 4 and Angle 3: These angles are adjacent and form a linear pair.
4. Angle 3 and Angle 1: These angles are adjacent and form a linear pair.
5. Angle 7 and Angle 8: These angles are adjacent and form a linear pair.
6. Angle 6 and Angle 8: These angles are adjacent and form a linear pair.
7. Angle 6 and Angle 5: These angles are adjacent and form a linear pair.
8. Angle 5 and Angle 7: These angles are adjacent and form a linear pair.

Linear Pairs Identified:
- (Angle 1, Angle 2)
- (Angle 2, Angle 4)
- (Angle 4, Angle 3)
- (Angle 3, Angle 1)
- (Angle 7, Angle 8)
- (Angle 6, Angle 8)
- (Angle 6, Angle 5)
- (Angle 5, Angle 7)

---

Step 2: Identify Vertically Opposite Angles

Vertically opposite angles are the angles that are opposite each other when two lines intersect. They are equal in measure.

1. Angle 1 and Angle 4: These angles are opposite each other.
2. Angle 2 and Angle 3: These angles are opposite each other.
3. Angle 5 and Angle 8: These angles are opposite each other.
4. Angle 6 and Angle 7: These angles are opposite each other.

Vertically Opposite Angles Identified:
- (Angle 1, Angle 4)
- (Angle 2, Angle 3)
- (Angle 5, Angle 8)
- (Angle 6, Angle 7)

---

Final Answer:

(i) Linear Pairs:
- (Angle 1, Angle 2)
- (Angle 2, Angle 4)
- (Angle 4, Angle 3)
- (Angle 3, Angle 1)
- (Angle 7, Angle 8)
- (Angle 6, Angle 8)
- (Angle 6, Angle 5)
- (Angle 5, Angle 7)

(ii) Vertically Opposite Angles:
- (Angle 1, Angle 4)
- (Angle 2, Angle 3)
- (Angle 5, Angle 8)
- (Angle 6, Angle 7)

---