In Fig. 6.16, if x+y=w+z, then prove that AOB is a line.
x+y+w+z=360∘ (angle at a point ).....(1)
x+y=w+z (given)....(2)
x+y+x+y=360∘ [from (1) and (2)]
2(x+y)=360∘⇒x+y=180∘
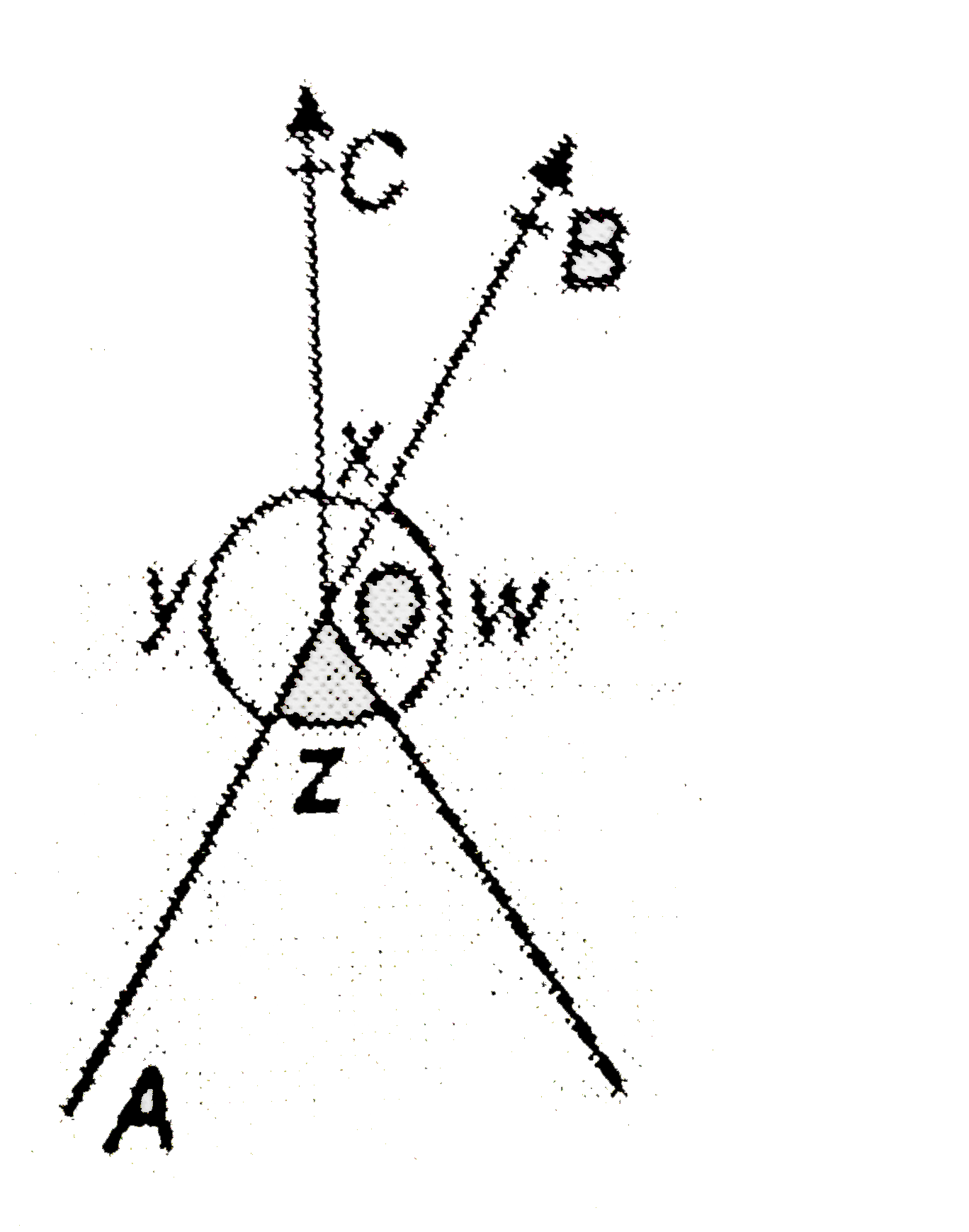
Hence, AOB is a straight line.
Topper's Solved these Questions
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6 A
19 Videos
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6 B
16 Videos
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Revision Exercise (long Answer Questions )
6 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Revision Exercise
12 Videos
- NUMBER SYSTEMBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - NUMBER SYSTEMEXERCISE - Revision Exercise (short Answer Questions)
10 Videos
Similar Questions
In Figure, if x+y=w+z, then prove that AOB is a line.
View SolutionIn Figure, if x+y=w+z, then prove that AOB is a line
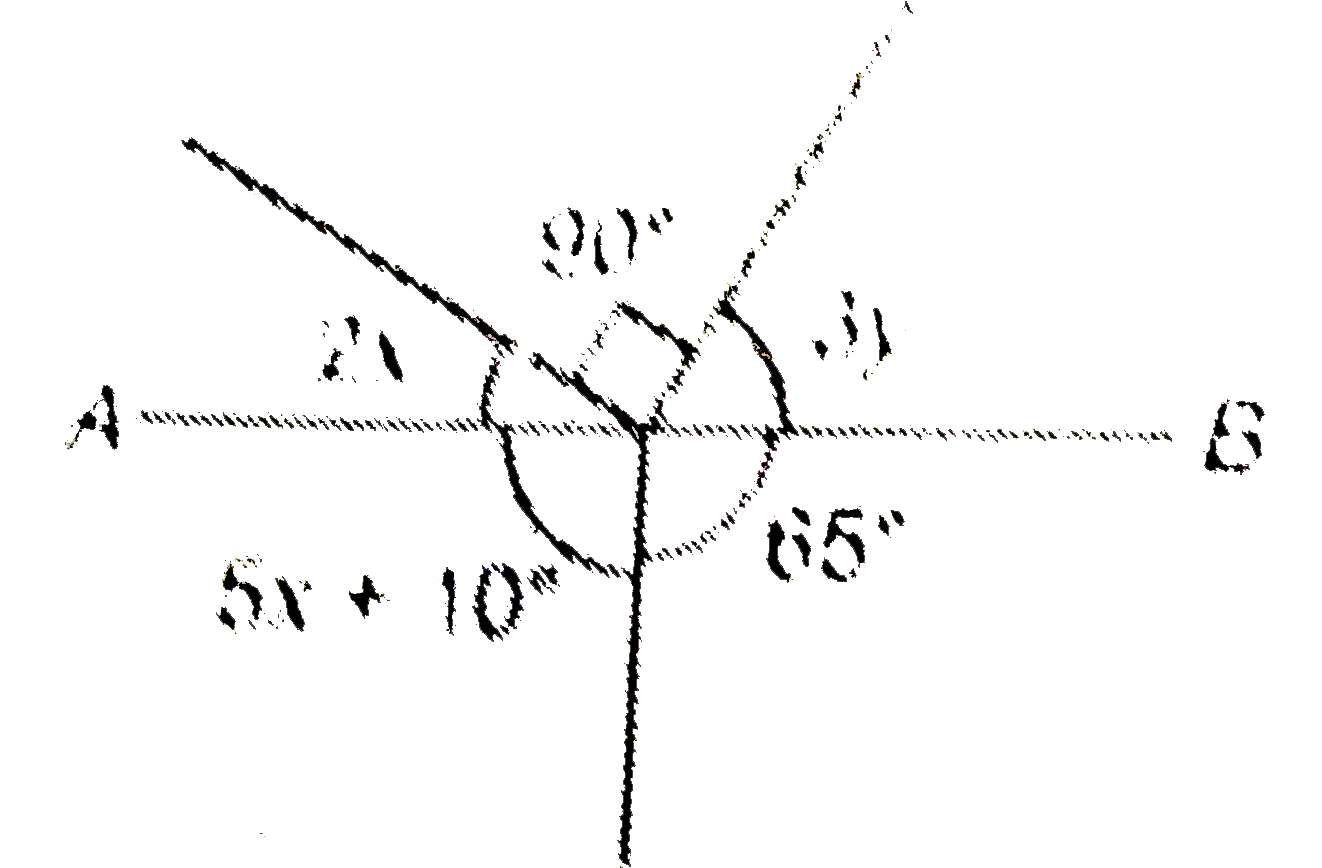
View SolutionIn the adjoining figure, find the values of x and y, Given that AOB is a straight line.
View SolutionIf z=z0+A(¯z−(¯z0)),whereA is a constant, then prove that locus of z is a straight line.
View SolutionFind the value of x if AOB is a straight line

View SolutionIf x,y,z are not all zero & if ax+by+cz=0,bx+cy+az=0&cx+ay+bz=0, then prove that x:y:z=1:1:1 OR 1:ω:ω2OR1:ω2:ω , where ω is one ofthe complex cube root of unity.
View SolutionIf the 4th, 10th and 16th terms of a G.P. are x, y, and z respectively. Prove that x, y, z are in G.P.
View SolutionIf z=x+iy and w=(1−iz)/(z−i) and |w|=1 , then show that z is purely real.
View SolutionIf ω≠1 is a cube root of unity and x+y+z≠0, then prove that ∣∣ ∣ ∣ ∣∣x1+ωyω+ω2zω2+1yω+ω2zω2+1x1+ωzω2+1x1+ωyω+ω2∣∣ ∣ ∣ ∣∣=0 if x=y=z
View SolutionIn given fig., if x3=y4=z5 , then calculate the values of x,y and z.
View Solution
