In Fig. 9.22, ABCD is a quadrilateral and BE ∣∣ ACand also BE meets DC produced at E. Show that area of ΔADEis equal to the area of the quadrilateral ABCD.
Lets proof BE||AC and take other things given.
area(ABCD)=area(ACD)+area(ABC)
area(ADE)=area(ACD)+area(AEC)
So, area(ABC)=area(AEC)
According theorem 9.2
BE||AC.
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise 9.2
6 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 9.4
8 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 9.1
1 Videos
- CIRCLESBOOK - NCERTCHAPTER - CIRCLESEXERCISE - EXERCISE 10.2
2 Videos
Similar Questions
Knowledge Check
In the adjoining figure, the area of quadrilateral ABCD is
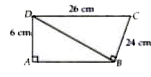 A148 cm2B144cm2C120 cm2D122 cm2
A148 cm2B144cm2C120 cm2D122 cm2ABCD is a cyclic quadrilateral. AB and DC are the chords, when produced meet in E. Then, what kind of ΔEBC and ΔEDA are ?
AEquilateralBEquiangularCCongurentDNone of the aboveIn the following figure AC=10&BD=14, then area of quadrilateral ABCD-
 A70√3B140√3C35√3D70
A70√3B140√3C35√3D70
In Fig. 9.22, ABCD is a quadrilateral and BE ∣∣ ACand also BE meets DC produced at E. Show that area of ΔADEis equal to the area of the quadrilateral ABCD.
View SolutionIn Figure, ABCD is a quadrilateral and BE⊥AC and also BE meets DC produced at E , Show that area of ADE is equal to the area of the quadrilateral ABCD.
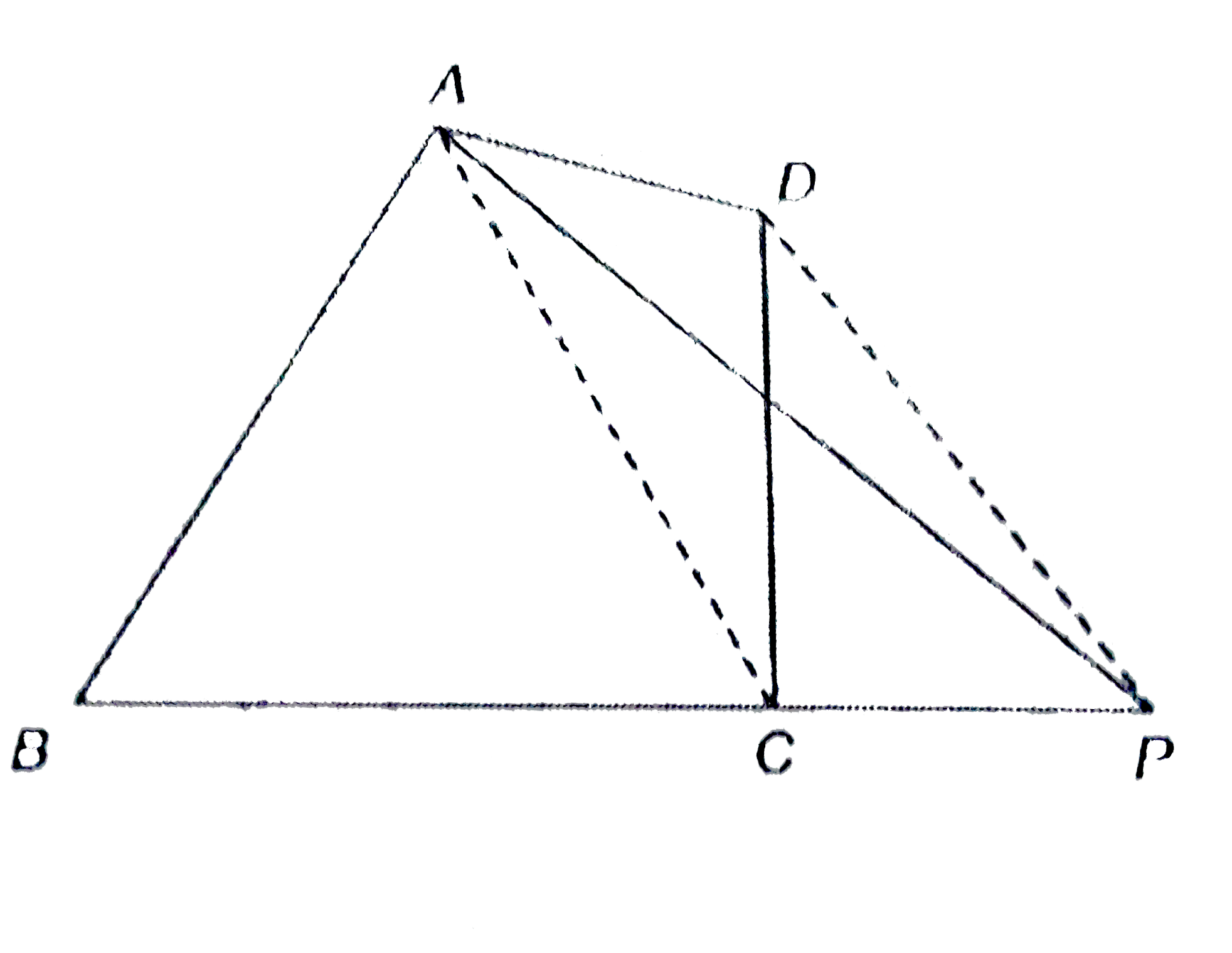
View SolutionIn the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
area of ΔABP= area of □ABCD
View SolutionThe given figure shows a pentagon ABCDE .drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F. Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
View SolutionIn quadrilateral ACBD, AC = ADand AB bisects ∠A(see Fig. 7.16). Show that ΔABC≅ΔABD

View Solution


