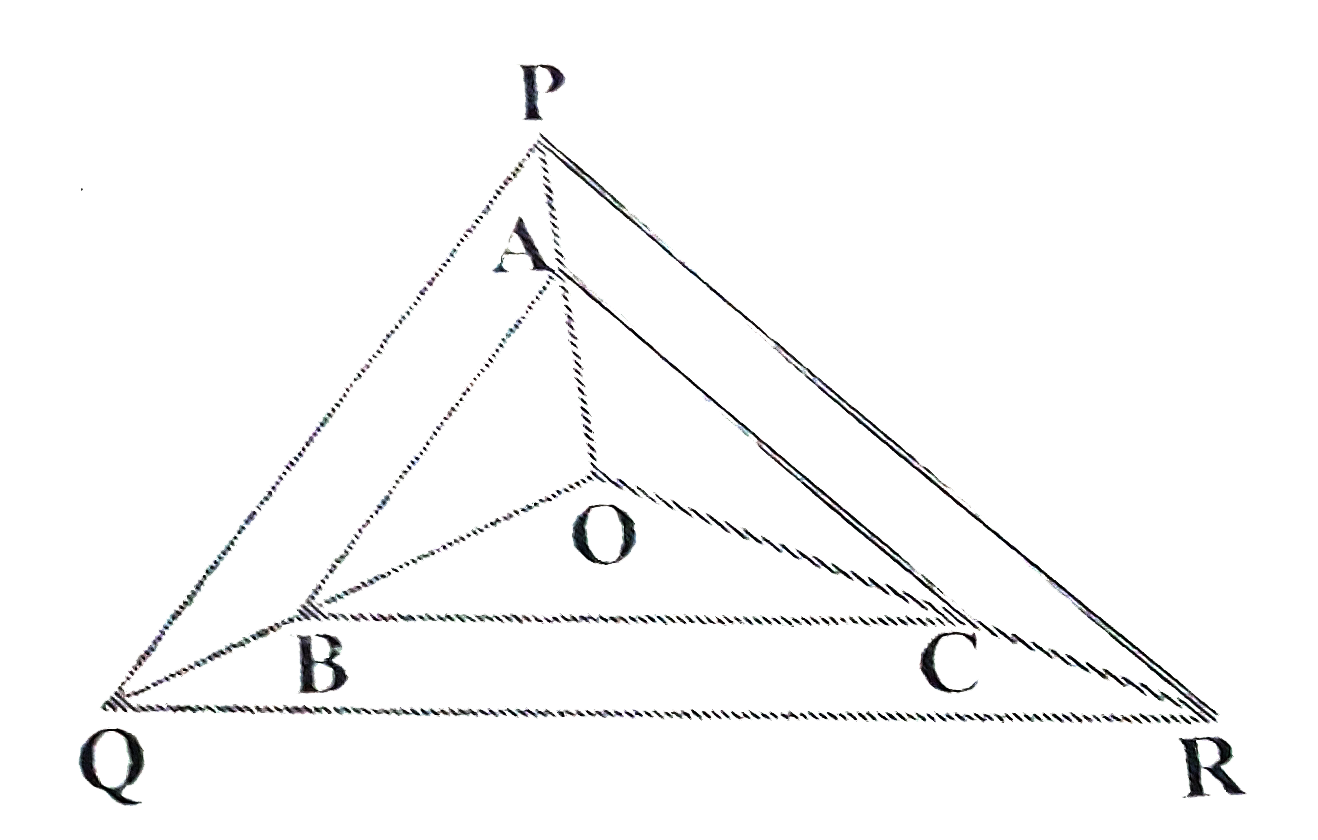
In figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
Video Solution
Text Solution
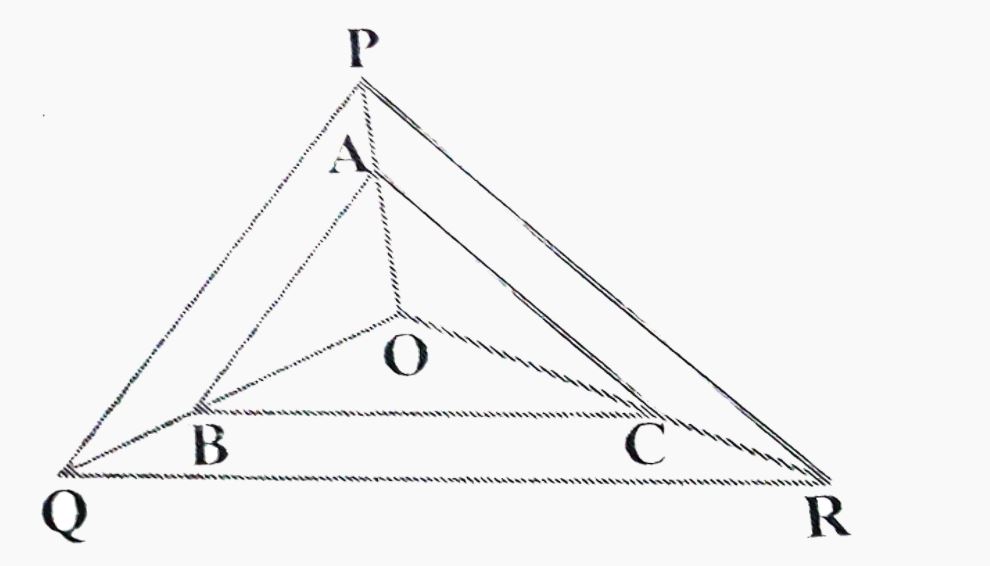
In ΔOPQ,
AB∣∣PQ (given)
OAAP=OBBQ .............. (i)
[By Basic proportionality theorem]
In ΔOPR
AC∣∣PQ (given)
OAAP=OCCR............. (ii) [By Basic proportionality theorem]
From equations (i) and (ii)
OAAP=OBBQ=OCCR
OBBQ=OCCR
Now, In ΔOQR
OBBQ=OCCR
Thus, BC∣∣QR [By Converse of Basic proportionality theorem]
|
Similar Questions
Knowledge Check
In triangle PQR, points A,B, and C are taken on PQ, PR and QR respectively such that QC=AC and CR=CB . If ∠QPR=40∘ then ∠ACB is equal to :
A140∘B40∘C70∘D100∘In △PQR, M and N are points on PQ and PR, respectively, such that ¯¯¯¯¯¯¯¯MN∣∣¯¯¯¯¯¯QR, If PM =x, PR =x+9,PQ=x+13 and PN=x−2, then find x.
A10B11C13D15
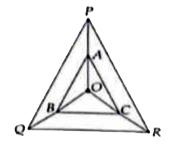
In the given figure points A, B, C respectively lie on sides OP, OQ such that AB||PQandAC||PR show that BC∣∣QR
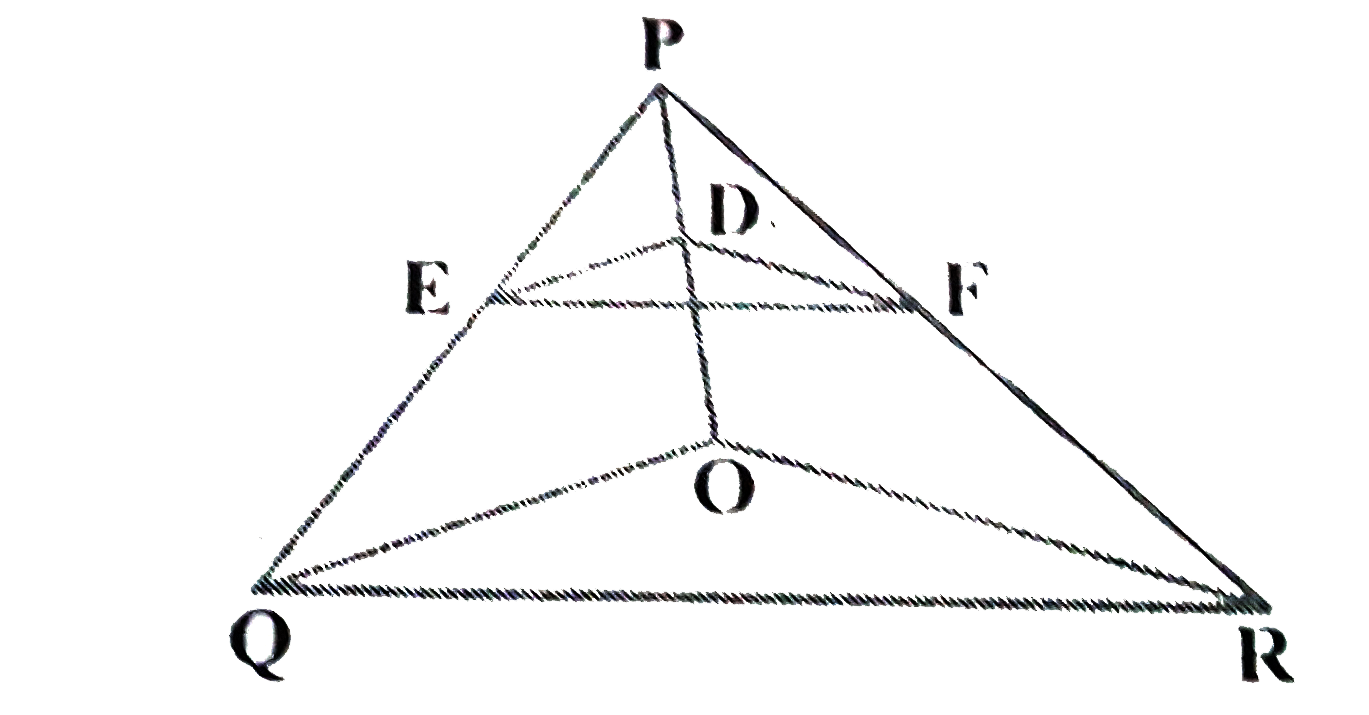
View SolutionIn figure DE || OQ and DF || OR. Show that EF||QR.
View SolutionIn a ABC,D and E are points on sides ABandAC respectively such that BD=CE. If ∠B=∠C, show that DEBC.
View SolutionIn figure, AB and CD are straight lines and OP and OQ are respectively the bisectors of angles ∠BOD and ∠AOC . Show that the rays OP and OQ are in the same line.
View SolutionIn Figure, ABC is a triangle in which AB=AC. Point DandE are points onthe sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View Solution□PQRS is a reactangle. If A, B and C are the mid-points of PQ, PS and QR respectively, then prove that
AB+AC=12(PR+SQ).
View Solution

