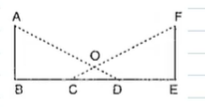
In Figure, AB⊥BC,FG⊥BC and DE⊥A⋅ Prove that triangle ADE~GCF
In△ADE and△GFC we have,
∠AED=∠GFC(right–∠s)
∠DAE=∠FGC(AD∣∣GFandACis∫ersec→r,similar∠s)
∴∠ADE=∠GCF(From∠∑∝ertyof△)
∴△ADE≅△GFC(By∀A≅ruencecriteria)
Topper's Solved these Questions
Similar Questions
In Figure, AB⊥BC,FG⊥BC and DE⊥AC.Provetˆ△ A D E~G C F
View SolutionIn Figure, AC=BC, ∠DCA=∠ECB and ∠DBC=EAC. Prove that triangle DBC and EAC are congruent, and hence DC=EC and BD=AE
View SolutionIn Figure, it is given that AB=EF,BC=DE,AB⊥BD and FE⊥CE. Prove that ABD≅FEC.
 View Solution
View SolutionIn Figure, it is given that AB=EF,BC=DE,AB⊥BD and FE⊥CE. Prove that ABD≅FEC.
View SolutionIn Figure, AB=AC and DB=DC. Prove that ∠ABD=∠ACD
View SolutionIn Figure, AC=AE, AB=AD and ∠BAD=∠EAC. Prove that BC=DE
View SolutionIn Figure, if BD⊥AC and CE⊥AB , prove that (i)△AEC~△ADB (ii)CAAB=CEDB
View SolutionIn Fig. 4.124, E is a point on side CB produced of an isosceles triangle ABC with AB=AC . If AD⊥BC and EF⊥AC , prove that (i) ABDECF (ii) AB×EF=AD×EC . (FIGURE)
View SolutionIn Figure, AB||CF and BC||ED . Prove that ∠ABC= ∠FDE
View SolutionIn figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.
 View Solution
View Solution

