In Figure, a is a greater than b by one third of a right-angle. Find the values of a and b.
To solve the problem, we need to find the values of angles a and b given that a is greater than b by one third of a right angle.
1. Understanding the relationship between a and b:
- We know that a is greater than b by one third of a right angle. A right angle is 90∘, so one third of a right angle is:
90∘3=30∘
- Therefore, we can express this relationship as:
a−b=30∘
- Rearranging this gives us:
a=b+30∘(Equation 1)
2. Using the fact that a and b are supplementary angles:
- Since a and b are angles on a straight line, they add up to 180∘:
a+b=180∘(Equation 2)
3. Substituting Equation 1 into Equation 2:
- We can substitute a from Equation 1 into Equation 2:
(b+30∘)+b=180∘
- Simplifying this gives:
2b+30∘=180∘
4. Solving for b:
- To isolate b, we subtract 30∘ from both sides:
2b=180∘−30∘
2b=150∘
- Now, divide both sides by 2:
b=150∘2=75∘
5. Finding a:
- Now that we have b, we can find a using Equation 1:
a=b+30∘=75∘+30∘=105∘
Final Values:
- Therefore, the values of a and b are:
a=105∘,b=75∘
- We know that a is greater than b by one third of a right angle. A right angle is 90∘, so one third of a right angle is:
90∘3=30∘
- Therefore, we can express this relationship as:
a−b=30∘
- Rearranging this gives us:
a=b+30∘(Equation 1)
- Since a and b are angles on a straight line, they add up to 180∘:
a+b=180∘(Equation 2)
- We can substitute a from Equation 1 into Equation 2:
(b+30∘)+b=180∘
- Simplifying this gives:
2b+30∘=180∘
- To isolate b, we subtract 30∘ from both sides:
2b=180∘−30∘
2b=150∘
- Now, divide both sides by 2:
b=150∘2=75∘
- Now that we have b, we can find a using Equation 1:
a=b+30∘=75∘+30∘=105∘
- Therefore, the values of a and b are:
a=105∘,b=75∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the figure, the area of rectangle EFGH is 3 units greater than the area of rectangle ABCD. What is the value of ab if a+b=8 ?
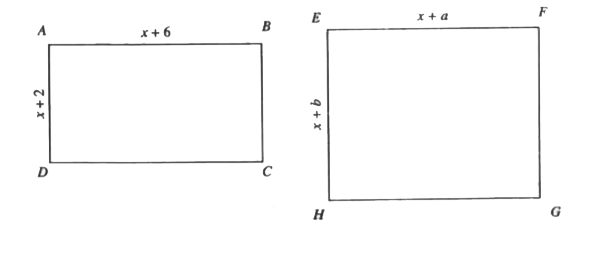 A9B12C15D18
A9B12C15D18
In Figure, AB∣∣CD. Find the value of x
 View Solution
View SolutionIn Figure, ABCD is a cyclic quadrilateral. Find the value of a and b.
View SolutionIn Figure, ABCD is a parallelogram. Find the values of xandy.
View SolutionIn Figure, BEST is a parallelogram. Find the values of x, y and z.
View SolutionThe points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right triangle, right-angled at B, Find the values of P.
View SolutionIn Figure, ACB is a line such that ∠DCA=5x and ∠DCB=4x. Find the value of x
View SolutionIn Figure, if AB∣∣CD find the value of x.
View Solution

