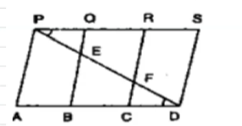
In Figure PQCD and PRCB. Prove that AQQD=ARRB.
In triangle A B C, we have
P Q 1 B C
So, by basic proportionality theorem, we have
AQAB=ADAC
In triangle A C D, we have
PRICD
There:ore, by basic proportionality theorem, we have
APAC=ARAD
From (i) and (ii), we obtain that
AQAB=ARAD { or }ARAD=AQAB { [Hence proved] }
=ABAQ=ADAR
=AQ+CBAQ=AR+RDAR
=1+QBAQ=1+RDAR
=QBAQ=DRAR [Hence proved]
Topper's Solved these Questions
Similar Questions
In Figure PQ∣∣CD and PR∣∣CB.ProveAQQD=ARRB.
View SolutionIn Fig. if PQ∣∣BC and PR∣∣CD . Prove that (i) ARAD=AQAB (ii) QBAQ=DRAR .
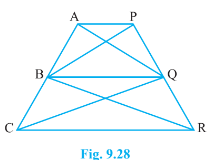
View SolutionIn Figure, AP||BQ ||CR. Prove that ar (AQC)= ar (PBR)
View SolutionIn Figure, PS=QR and ∠SPQ=∠RQP. Prove that PQS ≅ QPR, PR=QS and ∠QPR= ∠PQS
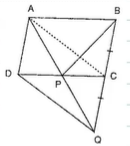
View SolutionIn Figure, PSDA is a parallelogram in which PQ=QR=RS and APBQCR. Prove that ar ( PQE)= ar ( CFD).
 View Solution
View SolutionIn Figure, ABCD and PQRC are rectangles and Q is the mid-point of AC . Prove that DP=PC (ii) PR=12 AC
View SolutionIn Figure, ABCD and PQRC are rectangles and Q is the mid-point of AC . Prove that DP=PC (ii) PR=12 AC
View SolutionIn Figure, ABCD is a parallelogram. Prove that: ar(BCP)=ar(DPQ) CONSTRUCTION : Join AC.
 View Solution
View SolutionIn Figure, ABCD is a parallelogram. Prove that: ar(BCP)=ar(DPQ) CONSTRUCTION : Join AC.
View SolutionIn Fig.9.28, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).
 View Solution
View Solution

