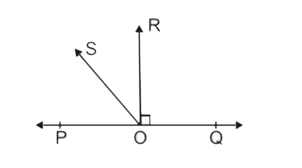
In figure POQ is a line. Raw Oris perpendicular to line PQ .OS is another ray lying between rays OP and OR. Prove that ∠ROS12(∠QOS−∠POS)i.e.,∠1=12(∠2−∠3)
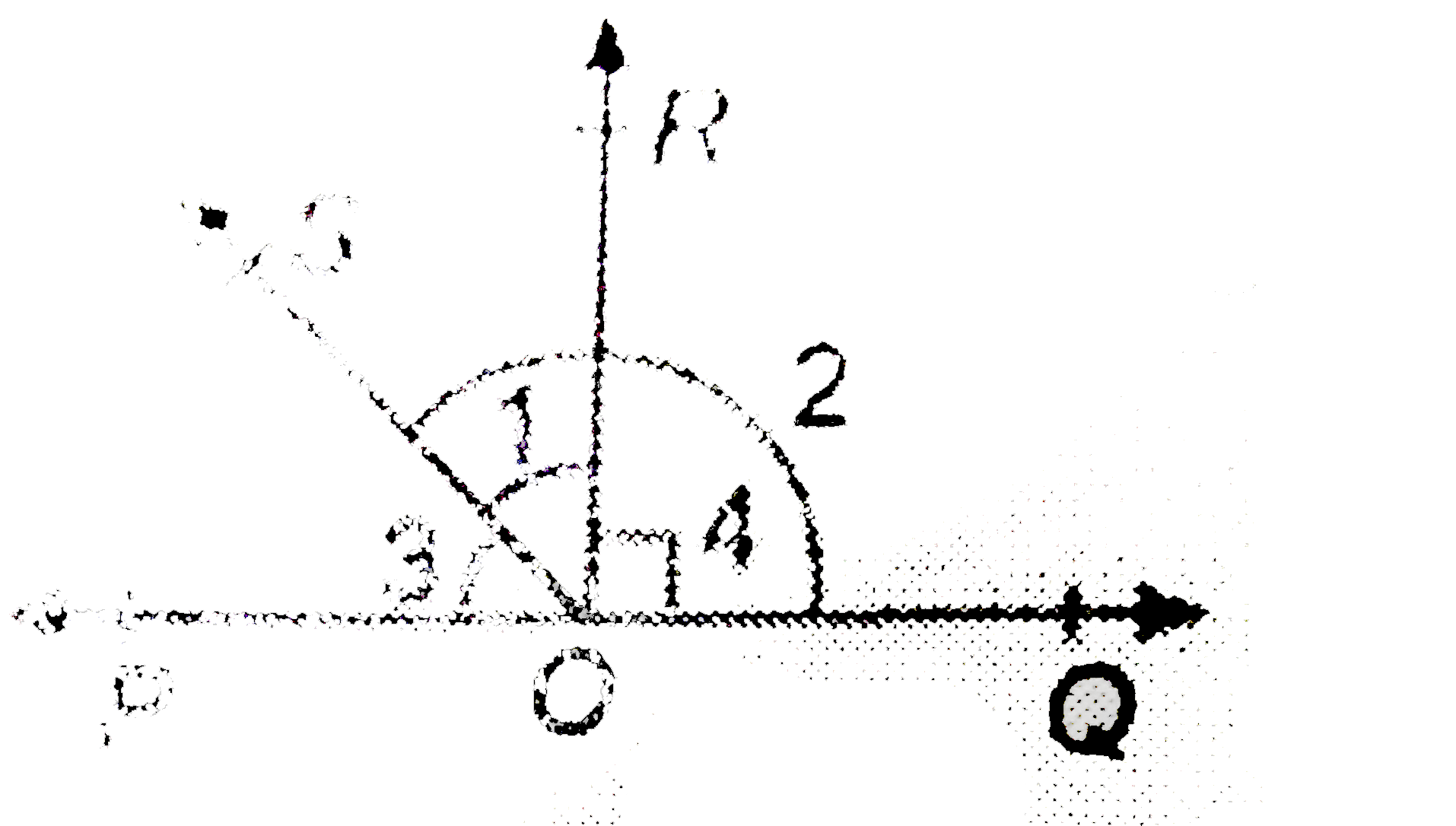
Since, Oris perpendicular to PQ
∴∠1+∠3=∠4
Now, ∠1=∠2−∠4 (each90∘).....(1)
⇒∠1=∠2−(∠1+∠3) (from the figure)
⇒∠1=∠2−∠1−∠3 [ from (1)]
⇒2∠1=∠2−∠3
⇒∠1=12(∠2−∠3)
Topper's Solved these Questions
- LINES AND ANGLESBOOK - NAGEEN PRAKASHANCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6 A
19 Videos
- LINES AND ANGLESBOOK - NAGEEN PRAKASHANCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6 B
16 Videos
- LINES AND ANGLESBOOK - NAGEEN PRAKASHANCHAPTER - LINES AND ANGLESEXERCISE - Revision Exercise (long Answer Questions )
6 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Revision Exercise
12 Videos
- NUMBER SYSTEMBOOK - NAGEEN PRAKASHANCHAPTER - NUMBER SYSTEMEXERCISE - Revision Exercise (short Answer Questions)
10 Videos
Similar Questions
In Figure, POQ is a line. Ray OR is perpendicular to lien PQ.OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS)
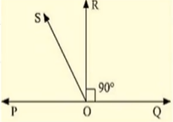
View SolutionIn Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS).
View Solution
Knowledge Check
What is the sum of all the angles of a 9 pointed star (i.e., ∠1+∠2+∠3+…..∠8+∠9)
A909∘B900∘C720∘D540∘
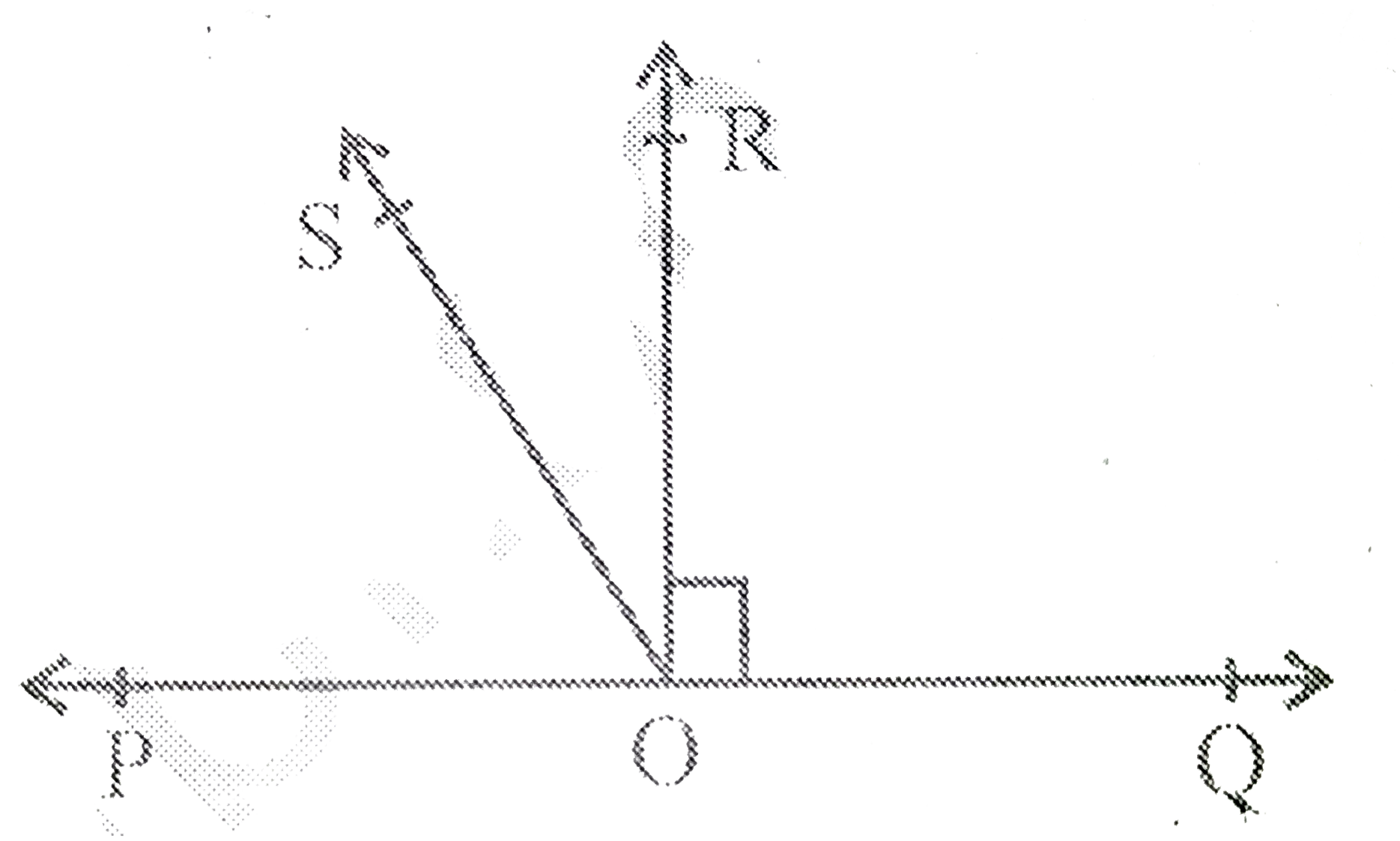
POQ is a straight line RO⊥PQ , SO is a ray from O then prove that ∠ROS=12(∠QOS−∠POS)
View SolutionProve that for any value of angle i, rays 1and2 are parallel

View SolutionIn Figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P. If angle POQ = 70°, then angleTPQ is equal to
View SolutionIn the given figure ,two straight line PQ and RS intersect at O.If ∠POS=114∘,find the measures of each of the angles :
∠POR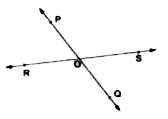
∠ROQ
∠QOS
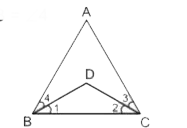
View SolutionIn given figure ∠ABC=∠ACBand∠3=∠4
Show that ∠1=∠2
View SolutionIn Figure, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ respectively. If ∠POS=x, find ∠ROT

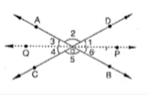
View SolutionIn figure, AB and CD are straight lines and OP and OQ are respectively the bisectors of angles ∠BOD and ∠AOC . Show that the rays OP and OQ are in the same line.
View Solution
