In figure, $△$ $A B C$ has sides $A B$ = $7.5$ $c m$ , $A C$ = $6.5$ $c m$ and $B C$ = $7$ $c m$ . On base $B C$ a parallelogram $D B C E$ of same area as that of $△$ $A B C$ is constructed. Find the height $D F$ of the parallelogram.

Video Solution

Text Solution

Verified by Experts

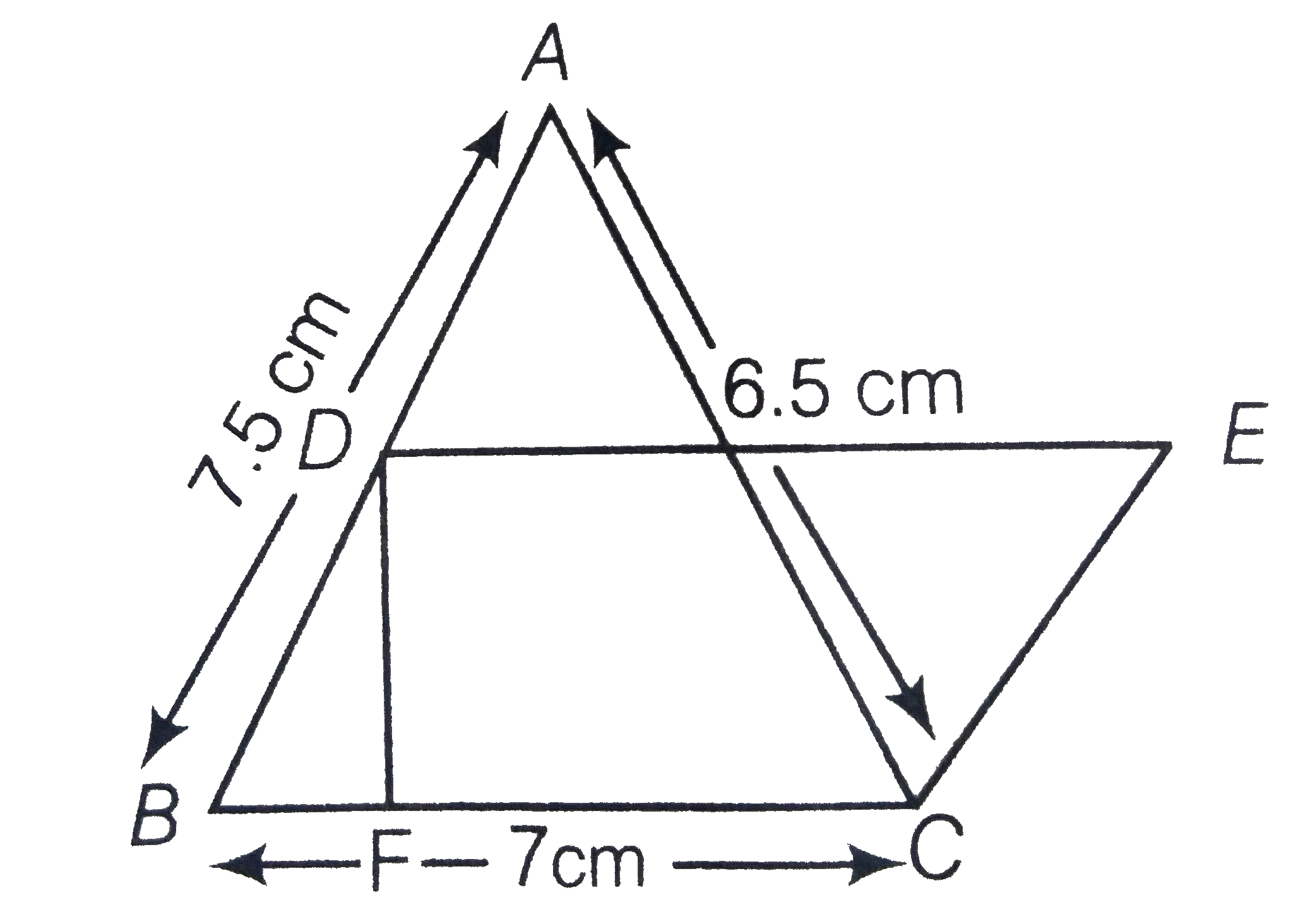
Now, first determine the area of $△$ ABC.
The sides of a triangle are
AB=a=7.5 cm, BC=b= 7 cm and CA=c=6.5 cm
Now, semi-perimeter of a triangle,
$s = \frac{a + b + c}{2} = \frac{7.5 + 7 + 6.5}{2} = \frac{21}{2} = 10.5 c m$
$∴ Area of △ A B C = \sqrt{s (s - a) (s - b) (s - c)} [by Heron's formula]$
$= \sqrt{10.5 (10.5 - 7.5) (10.5 - 7) (10.5 - 6.5)}$
$= \sqrt{10.5 \times 3 \times 35 \times 4} = \sqrt{441} = 21 c m^{2}$
Now, area of parallelogram $B C E D = Base \times Height$
$= B C \times D F = 7 \times D F$
According to the question,
Area of $△ A B C$ = Area of parallelogram BCED
$\Rightarrow 21 = 7 \times D F [from Eqs.(i) and (ii)]$
$\Rightarrow D F = \frac{21}{4} = 3 c m$
Hence, the height of parallelogram is 3 cm.

Updated on:21/07/2023

|

Class 9 MATHS HERONS FORMULA

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-HERON'S FORMULA-Long Answer Type Questions

Home
Ask Doubt
Profile