Question

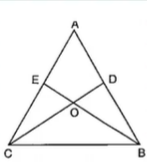
In Figure, two triangles ${\displaystyle ABC}$
and ${\displaystyle DBC}$
are on the same base ${\displaystyle BC}$
in which ${\displaystyle \angle A=\angle D={90}^0\stackrel{.}{}}$
If ${\displaystyle CA}$
and ${\displaystyle BD}$
meet each other at ${\displaystyle E,}$
show that ${\displaystyle AExCE=BExDE\stackrel{.}{}}$

Explanation

Given triangles {ABC} and {DBC} are {n} the same base {BC}.

Consider triangle 's {ABC} and {DBC}

`angle {A}=angle {D}=90^{circ}` (given)

`angle {AEB}=angle {DEC}` (vertically opposite angles are equal )

Hence,

triangle {ABC} sim triangle {DBC} (AA similarity theorem)


`Rightarrow frac{{AE}}{{DE}}=frac{{BE}}{{CE}} `

therefore `{AE} times {EC}={BE} times {ED}`