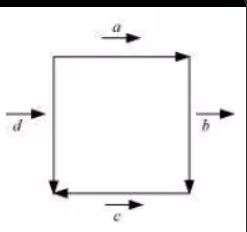
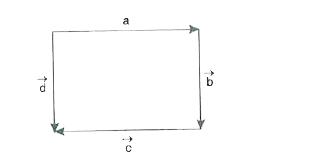
In Figure, which of the vectors are: (i) Collinear (ii) Equal (iii) Coinitial
(i)Vectors
→a
and
→d
are coinitial because they have the same initial point.
(ii) Vectors
→b
and
→d
are equal because they have the same magnitude and direction.
(iii) Vectors
→a
and
→b
are collinear but not equal as they are parallel, their directions are not the same.
Vectors
→b
and
→d
are collinear and equal vectors as they are parallel and their directions are same.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - NCERTCHAPTER - VECTOR ALGEBRAEXERCISE - EXERCISE 10.2
19 Videos
- VECTOR ALGEBRABOOK - NCERTCHAPTER - VECTOR ALGEBRAEXERCISE - MISCELLANEOUS EXERCISE
19 Videos
- VECTOR ALGEBRABOOK - NCERTCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise 10.5
7 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - NCERTCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - QUESTION
1 Videos
Similar Questions
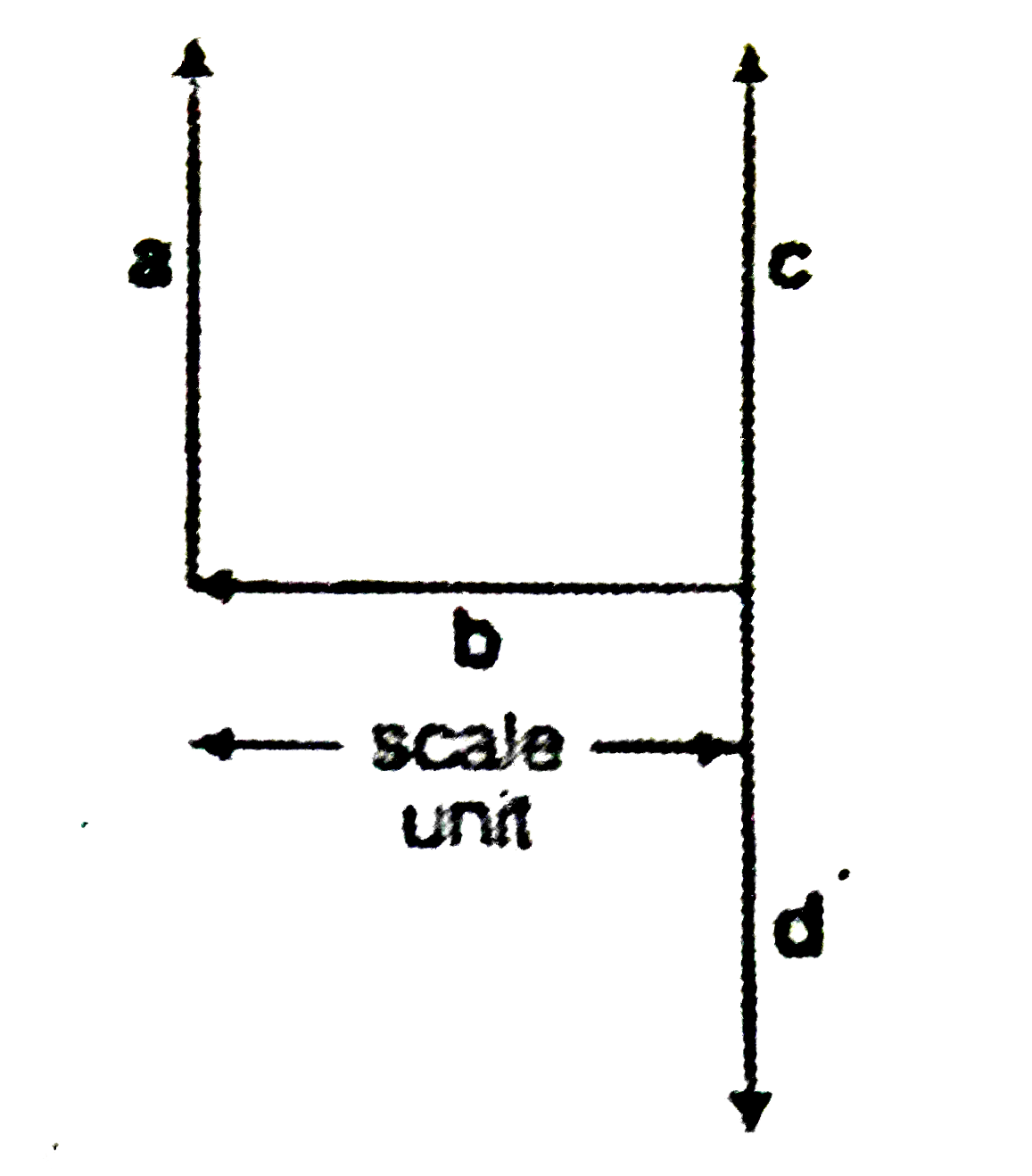
In the following figure, which of the vectors are:
(i) Collinear
(ii) Equal
(iii) Co-initial
(iv) collinear but not equal .
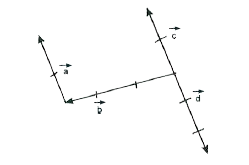
View SolutionIn the figure, which of the vectors are :
(i) Collinear
(ii) Equal
(iii) Co - initial.
View SolutionIn the given figure, which of the vectors are :
(a) Collinear
(b) Equal
(C ) Colinitial
View SolutionIn the given figure, ABCDEF is a regular hexagon, which vectors are:
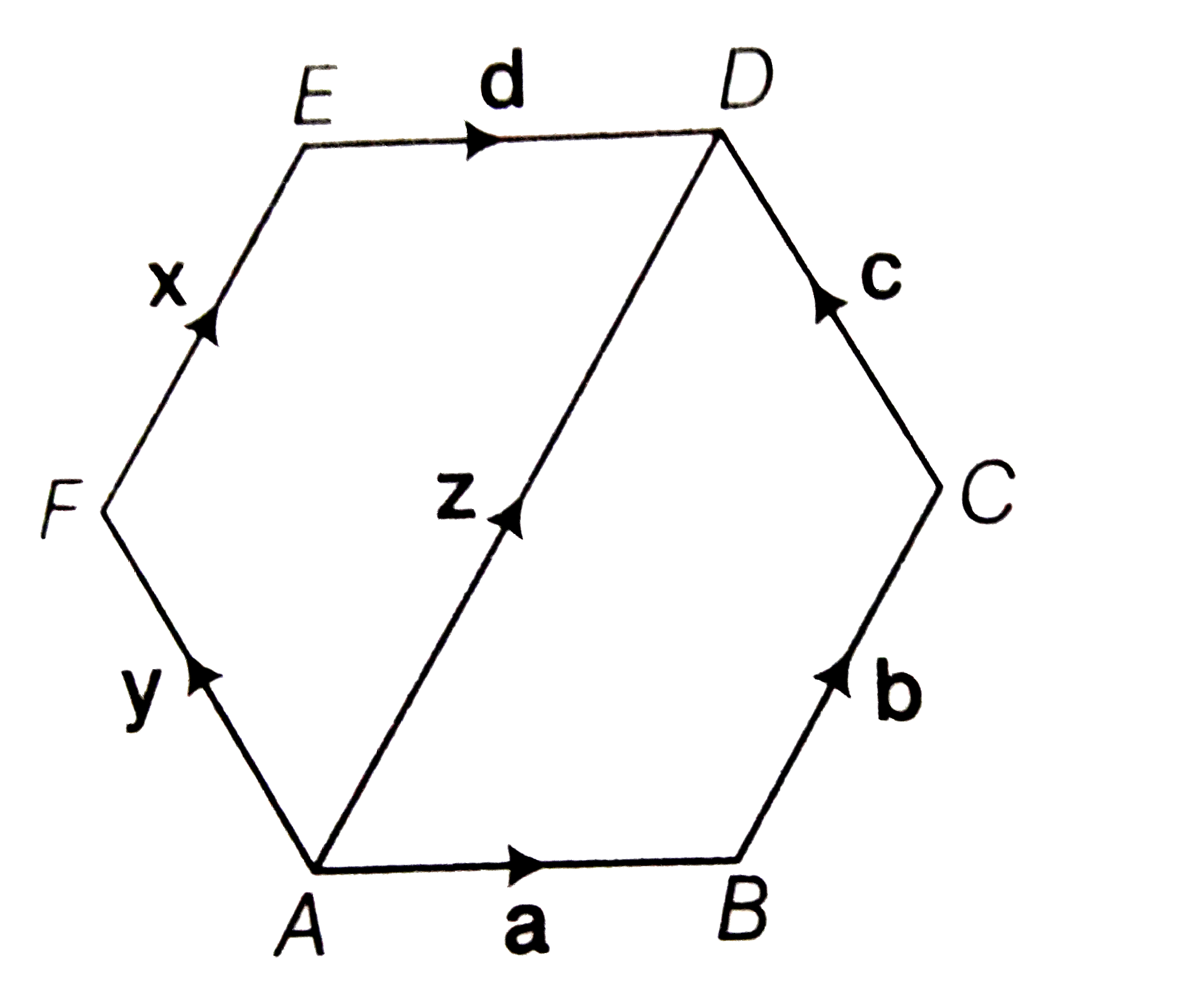
(i) Collinear
(ii) Equal
(iii) Coinitial
(iv) Collinear but not equal.
View SolutionIn fig 23.3, which of the vectors are: i.Collinear ii. Equal iii. Co-initial
View SolutionIn the adjoining figure which of the vector are: collinear
View SolutionIn the given figure, which of the following vector are
(a) collinear and equal (if ABCD are regular pentagon)
(b) coinitial vectors.
View SolutionIn the Fig., identify the following vectors :
(i) Coinitial
(ii) Equal
(iii) Collinear but not equal
View SolutionIn the figure, identify the following vectors :
(i) Co - initial
(ii) Equal
(iii) Collinear but not equal.

View SolutionIn Fig. ABCD is a regular hexagon, which vectors are: Collinear Equal Coinitial Collinear but not equal
View Solution
