In L.P.P., xj for all basic variable is equal to
1
−1
0
none of these
The correct Answer is:D
To solve the question "In L.P.P., xj for all basic variables is equal to...", we need to understand the concept of basic variables in the context of Linear Programming Problems (LPP).
1. Understanding Basic Variables:
In a Linear Programming Problem, we have a set of variables that are used to represent the decision variables in the objective function. The basic variables are those that correspond to the basic feasible solution of the linear programming model.
Hint: Remember that basic variables are those variables that are included in the solution of the system of equations formed by the constraints.
2. Formulating the Problem:
A standard LPP can be expressed in the form:
Maximize or Minimize Z=c1x1+c2x2+...+cnxn
subject to constraints like:
a11x1+a12x2+...+a1nxn≤b1
and the non-negativity constraints:
xj≥0 for all j
Hint: Identify the objective function and the constraints to understand the context of the problem.
3. Identifying Basic and Non-Basic Variables:
In the context of the simplex method, basic variables are those that are part of the solution (i.e., they have non-zero values), while non-basic variables are set to zero.
Hint: Basic variables are typically those that correspond to the pivot columns in the tableau during the simplex method iterations.
4. Values of Basic Variables:
The basic variables can take values that are either zero or positive. This means that for any basic variable xj, it can be expressed as:
xj≥0
However, it is not restricted to being exactly 0 or 1; it can take any non-negative value.
Hint: Recall that basic variables can be at their lower bound (0) or can take on any positive value depending on the constraints.
5. Conclusion:
Therefore, the statement "In L.P.P., xj for all basic variables is equal to..." can be concluded as:
- xj for basic variables can be either 0 or greater than 0.
The correct answer is that xj for all basic variables is equal to either 0 or a positive value.
Final Answer:
In L.P.P., xj for all basic variables is equal to either 0 or a positive value.
In a Linear Programming Problem, we have a set of variables that are used to represent the decision variables in the objective function. The basic variables are those that correspond to the basic feasible solution of the linear programming model.
A standard LPP can be expressed in the form:
Maximize or Minimize Z=c1x1+c2x2+...+cnxn
subject to constraints like:
a11x1+a12x2+...+a1nxn≤b1
and the non-negativity constraints:
xj≥0 for all j
In the context of the simplex method, basic variables are those that are part of the solution (i.e., they have non-zero values), while non-basic variables are set to zero.
The basic variables can take values that are either zero or positive. This means that for any basic variable xj, it can be expressed as:
xj≥0
However, it is not restricted to being exactly 0 or 1; it can take any non-negative value.
Therefore, the statement "In L.P.P., xj for all basic variables is equal to..." can be concluded as:
- xj for basic variables can be either 0 or greater than 0.
In L.P.P., xj for all basic variables is equal to either 0 or a positive value.
Topper's Solved these Questions
- LINEAR PROGRAMMING BOOK - ML KHANNACHAPTER - LINEAR PROGRAMMING EXERCISE - Question
2 Videos
- LIMITS, CONTINUITY AND DIFFERENTIABILITY BOOK - ML KHANNACHAPTER - LIMITS, CONTINUITY AND DIFFERENTIABILITY EXERCISE - MISCELLANEOUS EXERCISE (ASSERTION/ REASONS)
3 Videos
- LOGARITHMS AND SURDSBOOK - ML KHANNACHAPTER - LOGARITHMS AND SURDSEXERCISE - Miscellaneous exercise
3 Videos
Similar Questions
Knowledge Check
L.P.P. has constraints of
Aone variablesBtwo variablesCone or two variablesDtwo or more variablesThe equation (cosp−1)x2+cosp⋅x+sinp=0 where x is a variable, has real roots. Then the interval of possible values of p is
A(0,2π)B(−π,0)C(−π2,π2)D(0,π)Let A=[pqqp] such that det(A)=r where p,q,r all prime number, then trace of A is equal to
A6B5C2D3
The perimeter of a rectangle of length l and width w is given by the formula p=2(l+w)
The variables in the given formula are
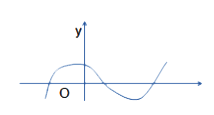
View SolutionThe following figure shows the graph of y=p(x), where p(x) is a polynomial in variable x. The number of zeroes of the polynomial p(x) is
View SolutionIf l,m are variable real numbers such that 5l2+6m2−4lm+3l=0 and the variable line lx+my=1 always touches a fixed parabola P(x,y)=0 whose axis parallel to x-axis , then A) vertex of P(x,y) is (-5/3, 4/3) B) Latus Rectum is equal to 4 C) Directrix of P(x,y) is parallel to y-axis (D) AB is a focal chord of P(x,y) =0 then 1SA+1SB=12 where S is the focus
View SolutionThe p.d.f. of a continuous random variable X is f(x)=K√x,0<x<4
= 0 , otherwise
Then P(X≥1) is equal to
View Solutionp1,p2,p3 are the distances of points (1,1),(2,0) and (0,2) from a variable line L such that p1+p2+p3=0. The line L passes through a fixed point
View Solution